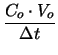Next: 2.3.3.5 Linear Inductor
Up: 2.3.3 Devices
Previous: 2.3.3.3 Linear Capacitor
The constitutive relation for a non-linear capacitor is
I = dQ/dt. Using the backward
Euler discretization scheme to discretize
dQ/dt one obtains
| I |
= |
 |
(2.37) |
| |
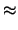 |
G . V - 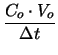 |
(2.38) |
| G |
= |
 |
(2.39) |
Equation (2.38) is a commonly used approximation
which, however, does not guarantee charge conservation [66,67]. For
constant C (2.38) of course simplifies to
(2.35). The stamp is given as
| yx, y |
 |
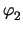 |
f |
| n1 |
G |
- G |
- I |
| n2 |
- G |
G |
I |
Tibor Grasser
1999-05-31