



Next: 3.1.2 The Drift-Diffusion Transport
Up: 3.1 Sets of Partial
Previous: 3.1 Sets of Partial
The basic equations are the Poisson
equation and continuity equations for electrons and holes.
div( . grad . grad  ) ) |
= q . (n - p - C) |
(3.2) |
| div Jn |
= q .  R + R + 
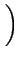 |
(3.3) |
| div Jp |
= - q .  R + R + 
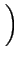 |
(3.4) |
The unknown quantities of this equation system are the electrostatic potential
 and the electron and hole concentrations n and p, respectively.
C denotes the net concentration of the ionized impurities,
and the electron and hole concentrations n and p, respectively.
C denotes the net concentration of the ionized impurities,  is the
dielectric permittivity of the semiconductor, and R is the net recombination
rate which has to be modeled properly.
is the
dielectric permittivity of the semiconductor, and R is the net recombination
rate which has to be modeled properly.
Tibor Grasser
1999-05-31