



Next: 4.3 The Full-Newton Algorithm
Up: 4. Simulator Coupling
Previous: 4.1.2 Modified Two-Level Newton
In [39] a method was proposed which was termed full-Newton algorithm.
However, this approach is very similar to the two-level method proposed
in the same paper hence it is termed ``quasi'' full-Newton in this thesis. The
basic idea will be demonstrated for the circuit shown in
Fig. 4.1. The combined device and circuit equations read
| f(x, V) |
= |
0 |
(4.13) |
| I(x, V) + G . (V - VS) |
= |
0 . |
(4.14) |
Applying Newton's method to (4.13) and (4.14)
one gets
 x . x . 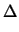 x + x +  V . V . 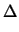 V V |
= |
- f(x, V) |
(4.15) |
 . . 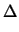 x + x +  . . 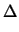 V + G . V + G . 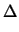 V V |
= |
- I(x, V) - G . (V - VS) . |
(4.16) |
Rearranging (4.15) yields
 x = x =  x-1 . x-1 .  - f(x, V) -
- f(x, V) -  V . V .  V V |
(4.17) |
which can be rewritten as
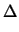 x x |
= |
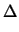  -
-  x-1 . x-1 .  V . V . 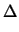 V V |
(4.18) |
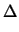  |
= |
-  x-1 . f(x, V) x-1 . f(x, V) |
(4.19) |
Substituting (4.18) in (4.16)
yields
 -
-  . .  x-1 . x-1 .  V + V +  + G .
+ G .   V = - V = -  . .   - I(x, V) - G . (V - VS) .
- I(x, V) - G . (V - VS) . |
(4.20) |
This equation can be rewritten as
 Geq + G Geq + G . .  V = - IT - G . (V - VS) V = - IT - G . (V - VS) |
(4.21) |
with
| Geq |
= |
-  . .  x-1 . x-1 .  V + V +  |
(4.22) |
| IT |
= |
 . . 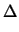  + I(x, V) .
+ I(x, V) . |
(4.23) |
Equation (4.21) is similar in form to that obtained
by the two-level Newton algorithm. Hence, similar methods can be used to embed
distributed devices into a circuit simulator and to provide a decoupling
between both simulators even for this quasi full-Newton algorithm.




Next: 4.3 The Full-Newton Algorithm
Up: 4. Simulator Coupling
Previous: 4.1.2 Modified Two-Level Newton
Tibor Grasser
1999-05-31