



Next: 5.7 Example
Up: 5. Contacts and Boundaries
Previous: 5.5 Contact Model
Having a separate solution variable for the contact voltage avoids numerical
problems with large arguments of the Bernoulli function B. Using
a Scharfetter-Gummel discretization scheme the expression for the
current between two grid points i and j reads
| Iij |
= |
C1 . (B(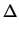 ) . nj - B(- ) . nj - B(- 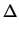 ) . ni) ) . ni) |
(5.25) |
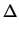 |
= |
C2 . ( -
-  ) + C3 ) + C3 |
(5.26) |
with Ci being material parameters. Applying the contact voltage directly
to the boundary grid point could cause large arguments of B and hence
numerical problems. This is avoided by having a separate variable for the
contact voltage. At the beginning of the iteration procedure the constitutive relation for
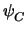 is violated and will only successively be adapted which guarantees
numerical stability (see Fig. 5.2).
is violated and will only successively be adapted which guarantees
numerical stability (see Fig. 5.2).
Figure 5.2:
Effect of a separate potential variable on the initial-guess of the
potential: a) with a separate potential variable the potential stays smooth
inside the semiconductor region. b) directly applying the contact potential
gives a large discontinuity of the potential.
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{a} {$\scriptstyle a)$...
...ncludegraphics[width=16cm,angle=0]{figures/sep-pot.eps}}\end{center}\end{figure}](img410.gif) |




Next: 5.7 Example
Up: 5. Contacts and Boundaries
Previous: 5.5 Contact Model
Tibor Grasser
1999-05-31
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{a} {$\scriptstyle a)$...
...ncludegraphics[width=16cm,angle=0]{figures/sep-pot.eps}}\end{center}\end{figure}](img410.gif)