



Next: B. Device Model Implementation
Up: Dissertation Grasser
Previous: 8. Outlook
A. Thermal Equivalents
Figure A.1:
a) Geometry and b) temperature distribution of a material block.
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{A} [c][c]{$\scriptsty...
...degraphics[width=16cm,angle=0]{figures/thermal-geo.eps}}\end{center}\end{figure}](img579.gif) |
Solving the one-dimensional static lattice heat flow equation
| div SL |
= |
H -  . cL . . cL . 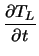 |
(A1) |
| SL |
= |
-  . grad TL . grad TL |
(A2) |
one can derive a thermal equivalent model for a device
with a geometry as shown in Fig. A.1a. With the boundary
conditions
TL(- a) = T1 and
TL(a) = T2 and under the assumption of
constant heat generation H the solution for the lattice temperature inside
the device reads
with
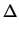 T T |
= T1 - T2, |
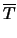 |
= 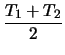 |
(A4) |
| PE |
= H . A . 2 . a, |
Gth |
=  . . |
(A5) |
It consists of a linear term arising from the boundary condition and a
quadratic term arising from heat generation inside the device due to the
dissipated electrical power PE. The temperature distribution is shown in
Fig. A.1b.
To derive a thermal equivalent circuit the discretized lattice heat flow
equation as solved by MINIMOS-NT can be used. Assuming constant electrical power
dissipation PE and a constant thermal heat capacity cL the
expression for a grid point i reads [36]
 Pi, j Pi, j |
= |
  + Cth .
+ Cth . 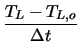 |
(A6) |
| Pi, j |
= |
Gth .  Ti - Tj Ti - Tj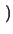 |
(A7) |
| Cth |
= |
Vi .  . cL . . cL . |
(A8) |
The sum in (A.6) considers the contribution of all neighbor
points j with Pi, j being the thermal heat flowing from point i to
point j. Using heat flows instead of electrical currents and temperatures
instead of voltages an electrical equivalent circuit can be used to model
(A.6). This equivalent circuit is shown in Fig. A.2
for grid point i in a two-dimensional situation with four neighbor points.
Figure A.2:
a) Grid point i and 4 neighbors used for the discretization of the lattice heat flow equation. b) Electrical analog circuit for the lattice heat flow equation.
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{a} {$\scriptstyle a)$...
...phics[width=16cm,angle=0]{figures/thermal-geo-grid.eps}}\end{center}\end{figure}](img596.gif) |
This equivalent circuit is approximately valid for the most general case. The
geometry of a schematic layout is shown in Fig. A.3.
To keep the problem tractable, device simulation is normally restricted to the
electrical active regions which make up only a small portion of the chip.
Heat generation is even further restricted to small areas of the device which
normally are the space charge regions for bipolar devices and the channel
regions for MOS devices. For other areas like buried collectors and
substrates heat generation is normally negligible as either the electric field,
the current density, or both are low. Therefore the heat generation term H
can be neglected for these areas and the thermal equivalent circuit reduces to
resistances and capacitances.
On the other hand, for the electrical active region the thermal resistances
and capacitances are of minor importance due to their small size. This is the
reason why power dissipation in electrical devices is normally modeled by a
power source alone which can be considered as reducing the power source to
a point source.
It is worthwhile to point out the simplifying assumptions made in the derivations
above:
- A constant thermal conductivity
 has been assumed which is a very
crude approximation. Using the exponential expression from [56]
has been assumed which is a very
crude approximation. Using the exponential expression from [56]
gives and error in the solution of the linear heat diffusion equation
in the order of 30 % [8].
- Heat generation has been assumed constant inside the device. This gives
a good approximation only when the temperature rise due to H is small compared
to the temperature rise induced by the boundary condition.
Figure A.3:
Electrical and thermal modeling of several transistors.
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{Electrical Region T1}...
...phics[width=16cm,angle=0]{figures/thermal-coupling.eps}}\end{center}\end{figure}](img601.gif) |




Next: B. Device Model Implementation
Up: Dissertation Grasser
Previous: 8. Outlook
Tibor Grasser
1999-05-31
![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{A} [c][c]{$\scriptsty...
...degraphics[width=16cm,angle=0]{figures/thermal-geo.eps}}\end{center}\end{figure}](img579.gif)
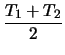
 .
.![\begin{figure}
\begin{center}
\resizebox{16cm}{!}{
\psfrag{a} {$\scriptstyle a)$...
...phics[width=16cm,angle=0]{figures/thermal-geo-grid.eps}}\end{center}\end{figure}](img596.gif)