4.7 Doping Dependence

This section tries to answer the question at which doping level one should measure if the effect is real. The dependence on the body doping is depicted in Fig. 4.20.

Figure 4.20: Drain currents of the SOI (Device 1) obtained by a energy transport simulations showing different body dopings $\textrm {N}_\textrm {A}$.

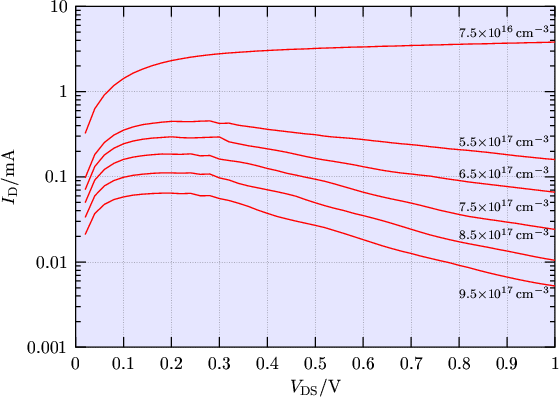The decrease of the drain current vanishes, if the doping is reduced by about one order of magnitude. A similar result has been reported in [56]. The doping-dependence of the simulated characteristics is difficult to interpret because several partial effects contribute. First, the body effect parameter which plays a key role increases with doping. Second, there is a doping-dependence introduced through the carrier lifetimes, which are modeled by the SCHARFETTER relation [59] [60]

$$\tau(N_\mathrm{i}) = \tau_\mathrm{min} + \frac{\tau_\mathrm{max} - \tau_\mathrm{min}} {1 + (N_\mathrm{i} / \mathrm{N}_\mathrm{ref})^\gamma} \ .$$ (4.2)

This is the default model in DESSIS (which was used in [56]) and it was also implemented and used in MINIMOS-NT. The advantage of this model is that with increasing doping concentration the lifetimes get reduced, which strengthens the coupling between the electron and hole subsystem, which in turn improves numerical stability. The same effect could be achieved by using small static lifetimes, but eqn. (4.2) provides a more physical model. The simulations show that with shorter lifetimes the negative differential conductance gets more pronounced, which corresponds well with the suggested explanation of the effect.

M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF