B. Driving Force Discretization

TO IMPLEMENT the discretization scheme described in Chapter 3 into the device simulator MINIMOS-NT an expression for the driving force was required. The driving force $\ensuremath{\boldsymbol{\mathrm{F}}}_n$ is defined by

$$\ensuremath{\boldsymbol{\mathrm{J}}}_n = \mathrm{q}\, \mu_n \, n \, \ensuremath{\boldsymbol{\mathrm{F}}}_n \ .$$ (B.1)

To obtain the discrete driving force the discretized current density eqns. (3.63) and (3.64)

$$J_n = - \frac{C_1}{\Delta x} \, \ensuremath{\overline{T_n}}\, \Bigl( ... .....}\ensuremath{\overline{T_n}}= \frac{\Delta T_n}{\ln(T_{n \, j} / T_{n \, i})}$$ (B.2)

$$Y_1 = - \frac{1}{\ensuremath{\overline{T_n}}} \, \Bigl( s_n \, \frac{\mathrm{q}}{\mathrm{k}_\mathrm{B}} \, \Delta \psi + \Delta T_n \Bigr) \ ,$$ (B.3)

must therefore be divided in some way by the electron concentration $n$. Thus, an average carrier concentration $\ensuremath{\overline{n}}$ is introduced via the following definition

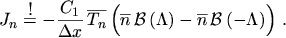$$J_n \stackrel{\textstyle !}{=} - \frac{C_1}{\Delta x} \, \ensurem... ...th{\overline{n}}\, \ensuremath{\mathcal{B} \left( - \Lambda \right) }\Bigr) \ .$$ (B.4)

By comparing the coefficients of eqn. (B.4) with those from eqn. (B.2)

$$\ensuremath{\overline{n}}\, \ensuremath{\mathcal{B} \left( \Lambda \right) } = n_j \, \ensuremath{\mathcal{B} \left( Y_1 \right) }\ ,$$ (B.5)

$$\ensuremath{\overline{n}}\, \ensuremath{\mathcal{B} \left( - \Lambda \right) } = n_i \, \ensuremath{\mathcal{B} \left( - Y_1 \right) }\ ,$$ (B.6)

and using the identity

$$\frac{\ensuremath{\mathcal{B} \left( x \right) }}{\ensuremath{\mathcal{B} \left( -x \right) }} = e^{-x} \ ,$$ (B.7)

the new argument $\Lambda$ of the BERNOULLI function can be calculated

$$e^{ -\Lambda} = \frac{n_j}{n_i} \, e^{- Y_1} \ ,$$ (B.8)

$$\Lambda = Y_1 - \ln(n_j / n_i) \ ,$$ (B.9)

and the average carrier concentration is finally found to be

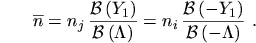$$\textcolor{lightgrey}{.......}\ensuremath{\overline{n}}= n_j \, \... ...\left( - Y_1 \right) }}{\ensuremath{\mathcal{B} \left( - \Lambda \right) }} \ .$$ (B.10)

Applying the identity

$$\ensuremath{\mathcal{B} \left( x \right) }- \ensuremath{\mathcal{B} \left( -x \right) }= -x \ ,$$ (B.11)

to eqn. (B.4) yields

$$J_n = - \frac{C_1}{\Delta x} \, \ensuremath{\overline{T_n}}\, \en... ...lta x} \, \ensuremath{\overline{T_n}}\, \ensuremath{\overline{n}}\, \Lambda \ .$$ (B.12)

After inserting $C_1$ from eqn. (2.188)

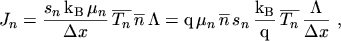$$J_n = \frac{s_n \, \mathrm{k}_\mathrm{B}\, \mu_n}{\Delta x} \, \e... ...{B}}{\mathrm{q}} \, \ensuremath{\overline{T_n}}\, \frac{\Lambda} {\Delta x} \ ,$$ (B.13)

the expression for the discretized driving force can easily be obtained

$$\boxed{ F_n = s_n \, \frac{\mathrm{k}_\mathrm{B}}{\mathrm{q}} \, ... ..._n}{\ln(T_{n \, j} / T_{n \, i})} \, \frac{Y_1 - \ln(n_j / n_i)}{\Delta x} }\ .$$ (B.14)

The consistency of the discretization can be checked by calculating the driving force in the limit of $\Delta x \to 0$

$$\lim_{\Delta x \to 0} F_n = \lim_{\Delta x \to 0} \, s_n \, \frac{\mathrm{k}_\mathrm{B}}{\m... ...\Delta x} - \frac{\ensuremath{\overline{T_n}}\, \Delta \ln(n)}{\Delta x} \Bigr)$$ (B.15)

$$= \lim_{\Delta x \to 0} \, s_n \, \frac{\mathrm{k}_\mathrm{B}}{\m... ...\frac{\Delta T_n}{\Delta \ln(T_n)} \, \frac{\Delta \ln(n)}{\Delta x} \Bigr) \ ,$$ (B.16)

where the abbreviations for $\Lambda$ and $Y_1$ have been expanded. Using the total derivative yields

$$F_n = - \ensuremath{\frac{\ensuremath{\mathrm{d}}\psi}{\ensuremath{\m... ...nsuremath{\frac{\ensuremath{\mathrm{d}}\ln(n)}{\ensuremath{\mathrm{d}}x}}\Bigr)$$ (B.17)

$$= E - s_n \, \frac{\mathrm{k}_\mathrm{B}}{\mathrm{q}} \, \frac{1}... ...\, \ensuremath{\frac{\ensuremath{\mathrm{d}}n}{\ensuremath{\mathrm{d}}x}}\Bigr)$$ (B.18)

$$= E - s_n \, \frac{\mathrm{k}_\mathrm{B}}{\mathrm{q}} \, \frac{1}... ...suremath{\frac{\ensuremath{\mathrm{d}}(n \, T_n)}{\ensuremath{\mathrm{d}}x}}\ ,$$ (B.19)

which is the one-dimensional projection of the driving force

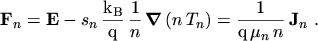$$\ensuremath{\boldsymbol{\mathrm{F}}}_n = \ensuremath{\boldsymbol{... ...\frac{1}{\mathrm{q}\, \mu_n \, n} \, \ensuremath{\boldsymbol{\mathrm{J}}}_n \ .$$ (B.20)

M. Gritsch: Numerical Modeling of Silicon-on-Insulator MOSFETs PDF