Definition A..8 (Lipschitz continuous)
A function
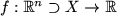
is said to be Lipschitz
continuous with Lipschitz constant

, if
Definition A..9 (Total Variation)
Let

be a decomposition of the interval
![$ [a,b]$](img66.png)
consisting of the
points

. If

is
function whose domain includes
![$ [a,b]$](img66.png)
, then
is called the variation of

with respect to

. If the upper
bound
![$ V(f,[a,b]) := \sup_Z V(f,Z)$](img755.png)
of the set of all variations
with respect to all decompositions of
![$ [a,b]$](img66.png)
exists, then
![$ V(f,[a,b])$](img65.png)
is called the total variation of

over
![$ [a,b]$](img66.png)
. In
this case

is of bounded variation.
Theorem A..10 (Weierstraß Approximation Theorem)
Let

be a real valued continuous function on the compact interval

. Then for each
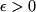
there is a polynomial

in
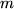
indeterminates
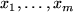
such that
Put differently, the set of all polynomials on

is dense in the
set of the real valued continuous function on the compact
interval

.
The Stone-Weierstraß Theorem is a generalization of the Weierstraß
Approximation Theorem [47].
Definition A..11
A family of real valued functions
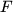
on

is said to separate the
points of

, if for two different points

and

of

there
is always an
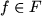
such that
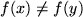
.
Theorem A..12 (Stone-Weierstraß, Formulation 1)
Let

be a compact subset of a normed space
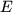
and

be a
subalgebra of

containing the function

and separating the
points of

. Then

is dense in

.
This is equivalent to the following formulation.
Theorem A..13 (Stone-Weierstraß, Formulation 2)
Let

be a compact subset of a normed space
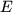
and

be a
closed subalgebra of

containing the function

and
separating the points of

. Then

.
Theorem A..14 (Taylor)
Let

(

open) be a

function and

be
an

-neighborhood of

lying in

. Then for all

with
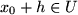
we have
where
Theorem A..15 (Generalized Taylor Series)
Let

(

open) be an analytical function.
Then
holds.
Clemens Heitzinger
2003-05-08
