2.3.1 Landauer Formula

According to the Landauer formalism [51], the electric current can be calculated using the electronic transmission function $\overline{T}_\mathrm{el}(E)$ :

$$I=\frac{2e}{h}\int_{-\infty}^{+\infty} \overline{T}_{\mathrm{el}}(E)\left [ f_{\mathrm{s}}(E)-f_{\mathrm{d}}(E) \right ] \ dE$$ (2.27)

Here, $f_{\mathrm{s,d}}(E)$ are the Fermi distribution functions of the source and drain contacts, respectively. In the linear response regime, the electrical current is proportional to the applied voltage:

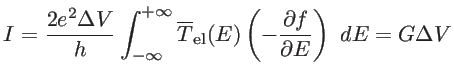$$I=\frac{2e^2\Delta V}{h}\int_{-\infty}^{+\infty} \overline{T}_{\mathrm{el}}(E)\left(-\frac{\partial f}{\partial E}\right) \ dE=G\Delta V$$ (2.28)

where the electrical conductance $G$ is defined as:

$$G=\frac{2e^2}{h}\int_{-\infty}^{+\infty}\overline{T}_\mathrm{el}(E)\left(-\frac{\partial f}{\partial E}\right)\ dE$$ (2.29)

The derivative of the Fermi function:

$$-\frac{\partial f}{\partial E} = \frac{1}{4k_{\mathrm{B}}T}\left ... ...{cosh} \left ( \frac{E-E_{\mathrm{F}}}{2 k_{\mathrm{B}}T}\right ) \right ]^{-2}$$ (2.30)

is known as the thermal broadening function, where $E_{\mathrm{F}}$ is the Fermi-level of the system. It has a width of a few $k_{\mathrm{B}}T$ around $E_{\mathrm{F}}$ , indicating that electrons around the Fermi energy have a major contribution to the electrical current.

Other than the applied voltage, a temperature difference can also result in a flow of charge carriers, as explained in Chapter 1. In the linear response regime, the electrical and heat currents are proportional to the applied voltage, when the temperature difference is zero. They are also proportional to the temperature difference, if there is no applied voltage. These currents are expressed as:

$$I=G\Delta V + \overline{SG}\Delta T$$ (2.31)

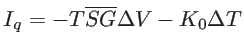$$I_q=-T\overline{SG}\Delta V -K_0\Delta T$$ (2.32)

where $I$ and $I_q$ are the electric and the heat current, respectively. Here, $K_0$ is the electronic contribution to the thermal conductivity for zero electric field, defined as [52]:

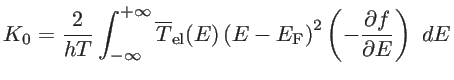$$K_0=\frac{2}{hT}\int_{-\infty}^{+\infty}\overline{T}_\mathrm{el}(E)\left(E-E_\mathrm{F}\right)^2\left(-\frac{\partial f}{\partial E}\right)\ dE$$ (2.33)

As we show later, the proportionality factor of the temperature difference $\Delta T$ in Eq. 2.31 is equal to the product $SG$ , where $S$ is the Seebeck coefficient and $G$ is the electrical conductance. We represent this factor by $\overline{SG}$ . Similarly, the proportionality factor of $\Delta V$ in Eq. 2.32 is represented by $-T\overline{SG}$ . Eqs. 2.31 and 2.32 can be rewritten as [30,52]:

$$\Delta V=I/G-S\Delta T$$ (2.34)

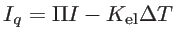$$I_q=\Pi I -K_{\mathrm{el}}\Delta T$$ (2.35)

where $\Pi=-TS$ is the Peltier coefficient and

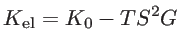$$K_{\mathrm{el}}=K_0-TS^2G$$ (2.36)

The Seebeck coefficient can be evaluated by $S=\overline{SG}/G$ as [52]:

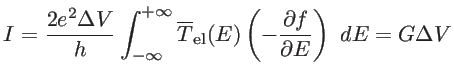
$$S=\frac{1}{-eT} \frac{\displaystyle{\int_{-\infty}^{+\infty}}\ove... ...}\overline{T}_{\mathrm{el}}(E)\left ( -\frac{\partial f}{\partial E} \right)dE}$$ (2.37)