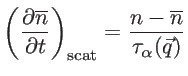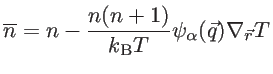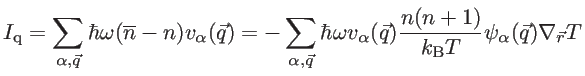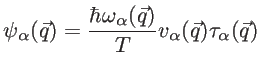Next: 3. Thermoelectric Properties of Graphene-Based Nanostructures
Up: 2.4 Phonon Transport
Previous: 2.4.1 Landauer Formula
Contents
At equilibrium, the distribution of phonons in branch  and wavevector
and wavevector  is given by the Bose-Einstein distribution function
is given by the Bose-Einstein distribution function  :
:
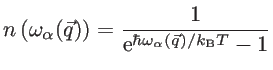 |
(2.59) |
Under non-equilibrium conditions, the distribution of phonons deviates from its equilibrium distribution, and transport of phonons is computed using the Boltzmann transport formalism. The non-equilibrium distribution function
 , in general, is a function of time
, in general, is a function of time  and position
and position  . The BTE can be written as:
. The BTE can be written as:
 |
(2.60) |
and for the steady state:
 |
(2.61) |
Under a temperature gradient, the BTE can be written as [60]:
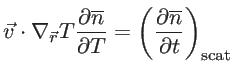 |
(2.62) |
In the relaxation time approximation, the change of the distribution function due to the scattering events can be given by:
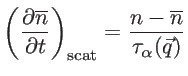 |
(2.63) |
and therefore
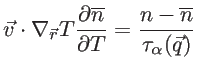 |
(2.64) |
where
 is the relaxation time of phonons of frequency
is the relaxation time of phonons of frequency
 . In this work we use a linearized
form of Eq. 2.64, which assumes that the temperature gradient causes only a
small deviation from Bose-Einstein distribution function [61,62], so that:
. In this work we use a linearized
form of Eq. 2.64, which assumes that the temperature gradient causes only a
small deviation from Bose-Einstein distribution function [61,62], so that:
 |
(2.65) |
and
 |
(2.66) |
where
 shows the deviation from the equilibrium distribution. Then, one may eliminate the temperature gradient using
shows the deviation from the equilibrium distribution. Then, one may eliminate the temperature gradient using
 and write:
and write:
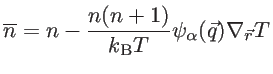 |
(2.67) |
Since the equilibrium distribution does not carry any heat flux, the heat flux equals
to [62]:
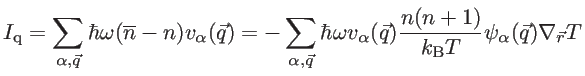 |
(2.68) |
On the other hand, it holds the differential form of Fourier's law:
 |
(2.69) |
Therefore, one can obtain the lattice thermal conductivity as:
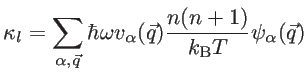 |
(2.70) |
Under the single-mode relaxation time (SMRT) approximation [62],
 follows from the linearized BTE (Eqs. 2.64-2.66) as:
follows from the linearized BTE (Eqs. 2.64-2.66) as:
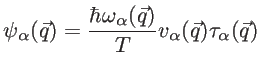 |
(2.71) |
Here,
 is the scattering time in SMRT approximation. Therefore, Eq. 2.70 becomes
is the scattering time in SMRT approximation. Therefore, Eq. 2.70 becomes
 |
(2.72) |




Next: 3. Thermoelectric Properties of Graphene-Based Nanostructures
Up: 2.4 Phonon Transport
Previous: 2.4.1 Landauer Formula
Contents
H. Karamitaheri: Thermal and Thermoelectric Properties of Nanostructures
![]() and wavevector
and wavevector ![]() is given by the Bose-Einstein distribution function
is given by the Bose-Einstein distribution function ![]() :
:
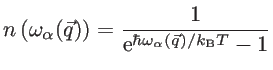
![]() , in general, is a function of time
, in general, is a function of time ![]() and position
and position ![]() . The BTE can be written as:
. The BTE can be written as: