5.2.1 Vertical Propagation Method

The vertical propagation method is the simplest imaging model. It is derived from the thin-film theory of Paul Berning [142] and was introduced into lithography simulation by Frederick Dill [141]. Early versions of the popular lithography simulators PROLITH [107] and SAMPLE [109] were based on it. The latent bulk image is obtained by the separation approach

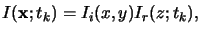$$I(\mathbf{x};t_k) = I_i(x,y) I_r(z;t_k),$$ (5.24)

whereby I_i(x, y) denotes the aerial image intensity and I_r(z;t_k) is the standing wave intensity inside the resist at a certain time-step t_k. For the computation of I_r(z;t_k) the resist is divided into thin layers over which the intensity and thus also the refractive index n(z;t_k) is approximately constant. Within one layer a technique similar to that described in Appendix C is employed to compute the field intensity. However, the method implicitly assumes that the field propagates only in vertical direction. For very low numerical apertures and reasonably thin resists this assumption is valid. It starts to fail when the aerial image changes or ``defocuses'' as it penetrates into the resist or when the incident light is appreciably oblique.