


 Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation
Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation
The time-dependent single-particle Schrödinger equation is
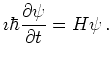 |
(6.1) |
Here  is the complex wave function.
The Hamiltonian operator
is the complex wave function.
The Hamiltonian operator  is a
Hermitian (self-adjoint) linear operator acting on the state space.
The Hamiltonian describes the total energy of the system.
is a
Hermitian (self-adjoint) linear operator acting on the state space.
The Hamiltonian describes the total energy of the system.
For a particle with
potential energy  the Hamiltonian is
the Hamiltonian is
If the effective mass  is space dependent we choose
the operator ordering
is space dependent we choose
the operator ordering
to get a self-adjoint Hamiltonian.
In all our applications the effective mass is piecewise
constant.
Position and momentum operators obey the
canonical commutation relations
![$\displaystyle [ X^{i}, P^{j} ] = \imath \hbar \delta^{ij} .$](img315.png) |
(6.4) |
In one-dimensional position space
 the position
operator
the position
operator  is given by
is given by
 (i.e., multiplication of
(i.e., multiplication of  by
by  ). The
momentum operator
). The
momentum operator  is then given by
is then given by
 .
With this the transient Schrödinger equation for the electron wave function
.
With this the transient Schrödinger equation for the electron wave function  on the real line
on the real line
 reads (with constant mass)
reads (with constant mass)
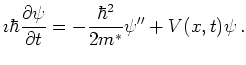 |
(6.5) |
In the so called time-independent case the wave
function is of the form
 |
(6.6) |
As time progresses, the state vectors change only by a complex phase
and Schrödinger's equation becomes an eigenvalue equation for the
Hamiltonian  ,
,
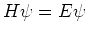 |
(6.7) |
or with 6.2
 |
(6.8) |
The inner product in the Hilbert space determines the
probabilistic structure. Observables are represented by
self-adjoint operators.
The inner product
 of
two vectors is given by
of
two vectors is given by
 |
(6.9) |
where we used Dirac's ``bra-ket'' notation.
The eigenvectors of the position operator are denoted by
 , we write
, we write  for the eigenvectors
of the momentum operator.
The wave functions
for the eigenvectors
of the momentum operator.
The wave functions  and
and  are then recovered as
are then recovered as
 |
(6.10) |
for abstract wave vectors  ,
,  .
The relation beween space and momentum representation is
a Fourier transformation
Observables are repesented by self-adjoint operators.
In the Dirac notation the expectation value of an
observable
.
The relation beween space and momentum representation is
a Fourier transformation
Observables are repesented by self-adjoint operators.
In the Dirac notation the expectation value of an
observable  given in state
given in state  is denoted by
is denoted by
 |
(6.11) |
Note that for non self-adjoint operators  the notation
the notation
 is ambiguous.
is ambiguous.



 Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation
Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation
R. Kosik: Numerical Challenges on the Road to NanoTCAD
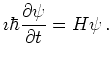
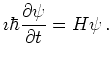
![]() is the complex wave function.
The Hamiltonian operator
is the complex wave function.
The Hamiltonian operator ![]() is a
Hermitian (self-adjoint) linear operator acting on the state space.
The Hamiltonian describes the total energy of the system.
is a
Hermitian (self-adjoint) linear operator acting on the state space.
The Hamiltonian describes the total energy of the system.
![]() the Hamiltonian is
the Hamiltonian is
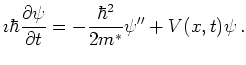

![]() of
two vectors is given by
of
two vectors is given by


![]()
![]()
![]()
![]() Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation
Previous: 6.1.1 Wave Mechanics
Up: 6.1.1 Wave Mechanics
Next: 6.1.1.2 Von Neumann Equation