previous up next contents Previous: 6.1.1.1 Schrödinger Equation Up: 6.1.1 Wave Mechanics Next: 6.1.2 Hydrodynamical Formulation

6.1.1.2 Von Neumann Equation

For quantum statistical mechanics the Schrödinger equation gives rise to the von Neumann equation for the density operator $ \rho$

$\displaystyle \imath \hbar \frac{\partial \rho}{\partial t} = [ H, \rho ] ,$ (6.12)

where the brackets denote the commutator

$\displaystyle [A,B] = AB - BA$ (6.13)

of operators $ A,B$. The density operator $ \rho$ is assumed self-adjoint, positive and of trace class. The density matrix $ \rho(x_1,x_2)$ is defined by

$\displaystyle \rho(x_1,x_2) = \langle x_1 \vert \rho \vert x_2 \rangle .$ (6.14)

For a pure state $ \psi$ the density operator is written in bracket notation as

$\displaystyle \vert\psi\rangle\langle\psi\vert$ (6.15)

and the corresponding matrix in position space is given by

$\displaystyle \rho(x_1, x_2) = \psi(x_1) \psi^*(x_2) . $

The probabilistic structure is now given by the trace operation $ {\mathrm{tr} }$. The expectation value of an observable $ A$ becomes

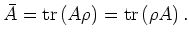$\displaystyle \bar{A} = {\mathrm{tr} (}A \rho) = {\mathrm{tr} (}\rho A) .$ (6.16)

previous up next contents Previous: 6.1.1.1 Schrödinger Equation Up: 6.1.1 Wave Mechanics Next: 6.1.2 Hydrodynamical Formulation

R. Kosik: Numerical Challenges on the Road to NanoTCAD