



Next: 2.3 Temperature and Electric
Up: 2. Mobility Models for
Previous: 2.1 Introduction
Subsections
Recently it has been realized that the carrier concentration
plays an important role for the mobility. Experiments show that for a hole-only diode and
a FET fabricated from the same conjugated polymer, the mobility could differ up
to three orders of the magnitude [41]. This
difference can only be explained by taking into account the dependence of mobility on the
carrier concentration. Rubel [42] analyzed this problem with the
concept of a transport energy  , but there is no direct proof for
the existence of such transport energy in organic systems. In this work we will focus
on extending the percolation model based on VRH theory by Vissenberg
[43] to explain the discrepancy of mobilities measured in OLEDs
and OFETs.
, but there is no direct proof for
the existence of such transport energy in organic systems. In this work we will focus
on extending the percolation model based on VRH theory by Vissenberg
[43] to explain the discrepancy of mobilities measured in OLEDs
and OFETs.
In this section, an analytical mobility model with a Gaussian DOS function has been obtained. It can explain the relation between the
mobility and carrier concentration. Results are in good agreement with
experimental data.
To calculate the mobility of an organic semiconductor, one can use
percolation theory, regarding such system as a random resistor network (network
of Miller and Abrahams) [7,44]. The current flows through the
bonds connecting the sites in the network. The conductance between the states  and
and  can be described as
can be described as
where  is a prefactor,
is a prefactor,
 is the Bohr radius of the
localized wave functions,
is the Bohr radius of the
localized wave functions,  is the temperature,
is the temperature,  and
and  denote the position and energy
of site
denote the position and energy
of site  . In theory the value of
. In theory the value of
 is determined by the threshold or critical conductance
is determined by the threshold or critical conductance  , at
which the first infinite cluster will form, given by the relation
, at
which the first infinite cluster will form, given by the relation
 |
(2.1) |
Here  is a prefactor. To describe the field-effect mobility in organic
transistors, Vissenberg assumed an exponential density of localized states
[43].
is a prefactor. To describe the field-effect mobility in organic
transistors, Vissenberg assumed an exponential density of localized states
[43].
 |
(2.2) |
 is the number of states per unit volume and
is the number of states per unit volume and  specifies the width of the
exponential distribution. Connecting (2.1) and (2.2), the conductivity can be
described as [43]
specifies the width of the
exponential distribution. Connecting (2.1) and (2.2), the conductivity can be
described as [43]
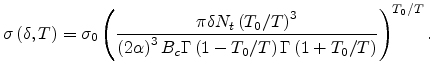 |
(2.3) |
Here  is the critical number
of bonds per site and
is the critical number
of bonds per site and  is the fraction of occupied states, defined as
is the fraction of occupied states, defined as
 is the gamma function. Then an expression for the mobility as a function of
the carrier concentration
is the gamma function. Then an expression for the mobility as a function of
the carrier concentration  can be obtained.
can be obtained.
 |
(2.4) |
However, this expression
can not account for the carrier concentration independent mobility when
the carrier concentration is very low (LED regime).
To overcome this problem, we derive another mobility model assuming a Gaussian DOS [9]
and VRH theory. In this model, the DOS function is given as
![$\displaystyle g\left(E\right)=\frac{N_t}{\sqrt{\pi}k_BT_{\sigma}}\exp\left[-\left(\frac{E}{k_BT_{\sigma}}\right)^2\right].$](img191.png) |
(2.5) |
Here  is the energy
measured relative to the center of the DOS and
is the energy
measured relative to the center of the DOS and
 indicates the width of the DOS. The
value of the Fermi energy
indicates the width of the DOS. The
value of the Fermi energy  can be determined by the
equation for the carrier concentration
can be determined by the
equation for the carrier concentration  .
.
 |
(2.6) |
At low concentration, the exponential
function is large compared to one (the nondegenerate case) [45], and
we obtain the Fermi energy as
 |
(2.7) |
According to percolation theory [17], at the onset of
percolation, the critical number  can be written as
can be written as
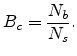 |
(2.8) |
 for a three-dimensional amorphous system,
for a three-dimensional amorphous system,  and
and  are, respectively, the density of bonds and density of sites in a
percolation system, which can be calculated as [43,46]
are, respectively, the density of bonds and density of sites in a
percolation system, which can be calculated as [43,46]
and
Here
 denotes the distance vector between sites
denotes the distance vector between sites  and
and  ,
,
 is the exponent of the conductance given by the relation
is the exponent of the conductance given by the relation
 [13] and
[13] and  is step function.
is step function.
Substituting (2.5) and (2.7) into (2.8), we obtain a new
percolation criterion for an organic system as
This equation has to be solved for  and an expression for mobility can be
obtained.
and an expression for mobility can be
obtained.
 |
(2.9) |
where
 is the Lambert function [47].
Equation (2.9) is obtained assuming
is the Lambert function [47].
Equation (2.9) is obtained assuming
- that the site positions are random,
- the energy barrier for the critical hop is large,
- and the charge carrier concentration is very low.
Figure 2.1:
Comparison between the analytical model (2.9) and empirical model
 for different temperature.
for different temperature.
|
|
Figure 2.4:
The calculated mobility versus carrier occupation at different
temperature.
|
|
Figure 2.5:
Comparison between calculation and typical experimental results
[41].
|
|
So far, much attention has been devoted to explain the temperature
dependence of the mobility [48,49,50].
As shown in Fig 2.1, the model (2.9) gives a non-Arrhenius-type
temperature dependence of the form
 , which has also been supported
by numerical simulations [51] and analytical calculations
[53]. The model (2.9) shows good agreement for a value
, which has also been supported
by numerical simulations [51] and analytical calculations
[53]. The model (2.9) shows good agreement for a value
 .
This value is close to
.
This value is close to
 given in
[52] and
given in
[52] and  in [53].
in [53].
In Fig 2.2, the mobility is plotted as a function of
 .
When plotted in this way, there exists the regime with a linear relation
between
.
When plotted in this way, there exists the regime with a linear relation
between  and
and  . This indicates that the
variable-range hopping effect has to be taken into account
[54,55].
. This indicates that the
variable-range hopping effect has to be taken into account
[54,55].
To obtain (2.7), a Boltzmann distribution function has been used. The degenerate limit of organic
semiconductors has been studied in [56,57]. In Fig 2.3 (a) we show the
Fermi energy for Boltzmann and Fermi-Dirac distributions assuming some typical
values
of the parameter
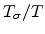 as 1.5, 3.5 and 6.0
[48].
Fig 2.3 (b) is a comparison especially for the higher carrier occupation regime.
The analytical result
(2.7) agrees well with the numerically calculated result for decreasing
carrier occupation and increasing
as 1.5, 3.5 and 6.0
[48].
Fig 2.3 (b) is a comparison especially for the higher carrier occupation regime.
The analytical result
(2.7) agrees well with the numerically calculated result for decreasing
carrier occupation and increasing
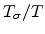 . Therefore, for the LED regime with low charge
carrier concentration, (2.7) is a good approximation of the solution of
(2.6).
. Therefore, for the LED regime with low charge
carrier concentration, (2.7) is a good approximation of the solution of
(2.6).
The mobility as a function of the carrier concentration is presented in Fig 2.4, where
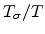 is in the range
is in the range  , corresponding to some typical values for organic
semiconductors. The mobility stays constant
until a certain threshold value of the carrier occupation. Above this threshold, the mobility can increase
about four orders of magnitude at
, corresponding to some typical values for organic
semiconductors. The mobility stays constant
until a certain threshold value of the carrier occupation. Above this threshold, the mobility can increase
about four orders of magnitude at
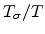
 9. These effects have also been
observed experimentally [41,58].
9. These effects have also been
observed experimentally [41,58].
However, (2.9) is valid only in the LED regime with very low
carrier concentration. As it is difficult to get an analytical expression for the
mobility at higher carrier concentration, we use (2.4) as the
mobility model for the higher carrier concentration. The
combined model can explain the experimental data in [41,58],
as shown in Fig 2.5.




Next: 2.3 Temperature and Electric
Up: 2. Mobility Models for
Previous: 2.1 Introduction
Ling Li: Charge Transport in Organic Semiconductor Materials and Devices


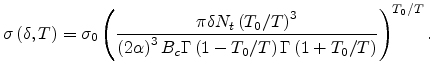

![]() can be written as
can be written as


![$\displaystyle B_c\approx\frac{2N_t\left(\sqrt{2}+1\right)\sqrt{\pi}}{\left(2\al...
...p\left(-\left[\frac{E_F+k_BTs_c}{k_BT_{\sigma}}\right]^2\right).\quad\quad\quad$](img202.png)
![$\displaystyle \eta=-\frac{T_\sigma}{T}\sqrt{-W\left[-\frac{B_c\left(2\alpha
T/T...
...gma\right)^3}{2\pi N_t\left(1+\sqrt{2}\right)}\right]}
-\frac{T_\sigma^2}{4T^2}$](img204.png)



![]() .
When plotted in this way, there exists the regime with a linear relation
between
.
When plotted in this way, there exists the regime with a linear relation
between ![]() and
and ![]() . This indicates that the
variable-range hopping effect has to be taken into account
[54,55].
. This indicates that the
variable-range hopping effect has to be taken into account
[54,55].
![]() as 1.5, 3.5 and 6.0
[48].
Fig 2.3 (b) is a comparison especially for the higher carrier occupation regime.
The analytical result
(2.7) agrees well with the numerically calculated result for decreasing
carrier occupation and increasing
as 1.5, 3.5 and 6.0
[48].
Fig 2.3 (b) is a comparison especially for the higher carrier occupation regime.
The analytical result
(2.7) agrees well with the numerically calculated result for decreasing
carrier occupation and increasing
![]() . Therefore, for the LED regime with low charge
carrier concentration, (2.7) is a good approximation of the solution of
(2.6).
. Therefore, for the LED regime with low charge
carrier concentration, (2.7) is a good approximation of the solution of
(2.6).
![]() is in the range
is in the range ![]() , corresponding to some typical values for organic
semiconductors. The mobility stays constant
until a certain threshold value of the carrier occupation. Above this threshold, the mobility can increase
about four orders of magnitude at
, corresponding to some typical values for organic
semiconductors. The mobility stays constant
until a certain threshold value of the carrier occupation. Above this threshold, the mobility can increase
about four orders of magnitude at
![]()
![]() 9. These effects have also been
observed experimentally [41,58].
9. These effects have also been
observed experimentally [41,58].