Next: 6. Space Charge Limited Up: 5. Charge Injection Models Previous: 5.2 Diffusion Controlled Injection

5.3 Charge Injection Model for OLED Based on Master Equation

The steady-state injection current in an OLED is the difference between the injection current from the electrode towards the organic semiconductor, $I_{inj}$ , and the recombination current, $I_{rec}$ , from the organic semiconductor back to the electrode. The first one is traditionally described by classical injection expressions, either FN or RS expression. In this work $I_{inj}$ and $I_{rec}$ enter of a master equation that describes the transport at the interface by a rate equation. This model yields the injection current as a function of electric field, temperature, energy barrier between metal and organic layer, and energetic width of the distribution of hopping sites. Good agreement with experimental data is found.

5.3.1 Theory

The system to be considered here is an energetically and positionally random hopping system in contact with a metallic electrode. At an arbitrary distance

away from the metal-organic layer interface, located at

, the electrostatic potential is given by the sum of the image charge potential and the applied potential described by electric field

as (5.1). Since the rapid variation of potential (5.1) takes place in front of the cathode, and space-charge effects can be ignored altogether in the calculation of the cathode characteristics [112,117], the field

may be regarded as being nearly constant.
Assuming no correlations between the occupation probabilities of different localized sates, the net electron flow between two states is given as

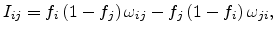$\displaystyle I_{ij}=f_i\left(1-f_j\right)\omega_{ij}-f_j\left(1-f_i\right)\omega_{ji},$

(5.11)

with

denoting the occupation probability of site

and $\omega_{ij}$ the electron transition rate of the hopping process between the occupied state

to the empty state

. The probabilities (5.11) are then employed in a master equation for describing charge transport. With the electrochemical potential $\mu'_i$ at the position of state

the occupation probability is described by a Fermi-Dirac distribution as

$\displaystyle f_i=\frac{1}{1+\exp\left(\frac{E_i'-\mu_i'}{k_BT}\right)}.$

(5.12)

For the metal electrode we assume a fixed electron concentration

and a Fermi-level of zero. All injected carriers are assumed to hop from the metal Fermi-level. Under the effect of a constant electric field

and the Coulomb field binding the carrier with its image charge on the electrode the energy and the electrochemical potential of a localized state are given by

$\displaystyle E_j'=E_j+\Delta-q\varphi\left(R_{j}, \theta\right), \mu_j'=\De... ...ht)=FR_{j}\cos\theta+\frac{q}{16\pi\epsilon R_{j}\cos\theta}% \qquad\quad\quad$

where $R_{j}$ denotes the distance of state

from the interface, $\theta$ the angle between

and $R_{j}$ , $\Delta$ the barrier height, and

the energy at state

without electric field. According to Mott's formalism [44], the transition rate $\omega_{j}$ from the metal Fermi-level to state

reads as

$\displaystyle \omega_{j}\propto\left\{\begin{array}{r@{\quad:\quad}l}\exp\left[... ...j'\ge 0 [6pt] \exp\left(-2\alpha R_{j}\right) & E_j'\leq 0 \end{array}\right.$

(5.13)

Connecting with a Gaussian DOS, the net current across the metal-organic contact can be written as

$\displaystyle I=I_{\rm inj}-I_{\rm rec}=e\nu_0\left(I_1+I_2-I_3-I_4\right)$

(5.14)

where $\nu_0$ is the attempt-to-jump frequency and

$\displaystyle I_1=\int_1^{+\infty}dr\int_{\beta}^{\infty}dR_j\int_{-\infty}^0dE... ...e\varphi\left(R_j,r\right)\right)\right)^2}{2\sigma^2}\right)\qquad\qquad\qquad$

$\displaystyle I_2=\int_1^{+\infty}dr\int_{\beta}^{\infty}dR_j\int_0^{\infty}dE_... ...(E_j-\left(\Delta-e\varphi\left(R_j,r\right)\right)\right)^2}{2\sigma^2}\right)$

$\displaystyle I_3=\int_1^{+\infty}dr\int_{\beta}^{\infty}dR_j\int_0^{\infty}dE_... ...(E_j-\left(\Delta-e\varphi\left(R_j,r\right)\right)\right)^2}{2\sigma^2}\right)$

$\displaystyle I_4=\int_1^{+\infty}dr\int_{\beta}^{\infty}dR_j\int_{-\infty}^0dE... ...(E_j-\left(\Delta-e\varphi\left(R_j,r\right)\right)\right)^2}{2\sigma^2}\right)$

where $r=1/\cos\theta$ , $\beta$ is the distance from the electrode to the first hopping site in the bulk and $f_j=\left(1+\exp\left(\frac{E_j-\mu_j}{k_BT}\right)\right)^{-1}$ .

and

describe the charge injection from the electrode downwards and upwards, respectively.

and

describe the backflow of charge to the electrode. The net current can be calculated by evaluating

and

numerically.

5.3.2 Results and Discussion

With the model presented we calculate the field dependence of the net, injection and backflow current. The parameters are $\Delta=0.3$ eV, $N_t=1\times 10^{22}$ cm $^{-3}$ ,

K, $\epsilon_r$ =3, $\beta=0.6$ nm, $\gamma=2\times 10^8$ cm $^{-1}$ , $\sigma=0.08$ eV and $\nu_0=1\times 10^{11}$ s $^{-1}$ . Fig 5.5 shows that with electric field the injection current increases and the backflow current decreases, as intuitively expected. As a result, the net current increases with electric field quickly in the low field regime.

Fig 5.6 shows a semilogarithmic plot of the current versus $F^{1/2}$ with the same parameters as used in Fig 5.5. This presentation is appropriate for testing RS behavior as $j\propto \exp\left(\sqrt{qF/{4\pi\epsilon\epsilon_0}}\right)$ . Since the dependence of $\log j$ versus $F^{1/2}$ is not linear, a deviation from the RS characteristics is observed.

Fig 5.7 shows the current-field characteristics for different $\Delta$ and $\nu_0=9\times 10^{11}$ s $^{-1}$ , the other parameters are the same as in Fig 5.5. The injection current increases with decreasing barrier height $\Delta$ and with electric field. The comparison between calculation and experimental data of DASMB sandwiched between ITO and Al electrodes [112] is given in Fig 5.8. The parameters are $\Delta=0.4$ eV and K, the other parameters are the same as in Fig 5.5. The agreements is quite good at low electric fields. The discrepancy between calculation and experimental data comes from the resistance of the ITO contact at high electric field [112].

**Figure 5.5:** Field dependence of the net, injection, and backflow currents.
$\resizebox{0.85\linewidth}{!}{\includegraphics{figures/injection/master/11.eps}}$

**Figure 5.6:** Relation between injection current and $F^{1/2}$ .
$\resizebox{0.83\linewidth}{!}{\includegraphics{figures/injection/master/12.eps}}$

**Figure 5.7:** Barrier height dependence of the injection current.
$\resizebox{0.83\linewidth}{!}{\includegraphics{figures/injection/master/2.eps}}$

**Figure 5.8:** Comparison between calculation and experimental data at .
$\resizebox{0.85\linewidth}{!}{\includegraphics{figures/injection/master/3.eps}}$

Next: 6. Space Charge Limited Up: 5. Charge Injection Models Previous: 5.2 Diffusion Controlled Injection

Ling Li: Charge Transport in Organic Semiconductor Materials and Devices