3.2.2.1 Phenomenological Approach

Figure 3.3: Illustration of the book-keeping character of Boltzmann's equation for one $\ensuremath {\ensuremath {\mathitbf {r}}}$ - and $\ensuremath {\ensuremath {\mathitbf {p}}}$ -dimension. Possible transitions are a spatial flux of carriers, a change of the carrier's momentum due to an external generic force, and scattering processes, after [73].

Since the Boltzmann transport equation represents a book-keeping equation for the distribution function, it can be derived from a phenomenological point of view illustrated in Fig. 3.3 for each spatial and momentum dimension. The net increase of carriers within the volume $\Delta r \Delta k$ can only be caused by a net in-flux of carriers in both real and momentum space or net in-scattering. Thus, the change of carriers within the volume $\Delta r \Delta k$ during the time window $\Delta t$ reads

$$\Delta \ensuremath{f}\Delta r \hbar \Delta k = \left(\ensuremath{f}(r)-\ensuremath{f}(r+\Delta r)\right) v \hbar \Delta k \Delta t$$ (3.5)

$$+ \left(\ensuremath{f}(\hbar k)-\ensuremath{f}(\hbar k + \hbar \Delta k)\right) F \Delta r \Delta t$$

$$+ \ensuremath{\ensuremath{\mathcal{Q}(\ensuremath{f})}}\Delta r \... ...h{\ensuremath{\mathcal{R}(\ensuremath{f})}}\Delta r \hbar \Delta k \Delta t \,,$$

with the velocity in real space $v$ and $F$ as a generic force. Scattering is expressed with the scattering operators $\ensuremath{\ensuremath{\mathcal{Q}(\ensuremath{f})}}$ and $\ensuremath{\ensuremath{\mathcal{R}(\ensuremath{f})}}$ , whereby the latter comprises inter-band processes and thus represents generation and recombination of free carriers in the semiconductor. Letting $\Delta r$ , $\Delta k$ , and $\Delta t$ become infinitesimal small and rearranging the equation leads to the one-dimensional Boltzmann transport equation

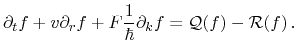$$\ensuremath{\ensuremath{\partial_{t} f}} + v \ensuremath{\partial... ...{Q}(\ensuremath{f})}}- \ensuremath{\ensuremath{\mathcal{R}(\ensuremath{f})}}\,.$$ (3.6)

Reformulation of (3.6) for three spatial and momentum dimensions yields

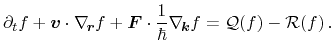$$\ensuremath{\ensuremath{\partial_{t} f}} + \ensuremath{\ensuremat... ...{Q}(\ensuremath{f})}}- \ensuremath{\ensuremath{\mathcal{R}(\ensuremath{f})}}\,.$$ (3.7)

Inserting Eqs. (3.2) and (3.3) into (3.7) delivers the commonly used form of the Boltzmann transport equation

$$\ensuremath{\ensuremath{\partial_{t} f}} + \ensuremath{\frac{1}{\... ...{Q}(\ensuremath{f})}}- \ensuremath{\ensuremath{\mathcal{R}(\ensuremath{f})}}\,.$$ (3.8)

The introduction of a formulation using Poisson brackets enables a compact and convenient notation incorporating useful identities. The definition of Poisson brackets as well as important properties are given in Section A. For the distribution function and the total energy, the Poisson bracket's definition (A.1) reads

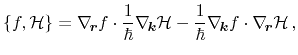$$\ensuremath{\{f,\ensuremath{{\cal{H}}}\}} = \ensuremath{\ensurema... ...{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}{\ensuremath{{\cal{H}}}} \,,$$ (3.9)

which enables the formulation of (3.8) in the compact form of

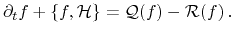$$\ensuremath{\ensuremath{\partial_{t} f}} + \ensuremath{\{f,\ensur... ...{Q}(\ensuremath{f})}}- \ensuremath{\ensuremath{\mathcal{R}(\ensuremath{f})}}\,.$$ (3.10)

The left side of the equation describes the ballistic behavior of the particle influenced by the generic force $F$ . The Poisson bracket $\ensuremath{\{f,\ensuremath{{\cal{H}}}\}}$ is also often referred to as the drift term of the Boltzmann transport equation. The generic force incorporates the sum of all considered driving forces to the particle, namely the electric field, a temperature gradient, as well as a position dependent band structure. The Lorentz force $\ensuremath{\ensuremath{\mathitbf{v}}}\ensuremath{\times}\ensuremath{\ensuremath{\mathitbf{B}}}$ describing the influence of a magnetic field is not taken into account in this work.

Statistical collisions interrupt the ballistic motion of the particles which are described by the collision term at the right side of Boltzmann's equation. The collision term incorporates both in-scattering from $\ensuremath{\ensuremath{\mathitbf{p}}}'$ to $\ensuremath {\ensuremath {\mathitbf {p}}}$ as well as out-scattering from $\ensuremath {\ensuremath {\mathitbf {p}}}$ to $\ensuremath{\ensuremath{\mathitbf{p}}}'$ . Thus it can be formulated as [73]

$$\ensuremath{\ensuremath{\mathcal{Q}(\ensuremath{f})}}= \sum_{\ens... ...uremath{\ensuremath{\mathitbf{p}}},\ensuremath{\ensuremath{\mathitbf{p}}}') \,,$$ (3.11)

where $\ensuremath{f}(\ensuremath{\ensuremath{\mathitbf{p}}}')$ denotes the probability for the state at $\ensuremath{\ensuremath{\mathitbf{p}}}'$ to be occupied and $\left(1-\ensuremath{f}(\ensuremath{\ensuremath{\mathitbf{p}}}) \right)$ the probability for the state at $\ensuremath {\ensuremath {\mathitbf {p}}}$ to be available for in-scattering. $S(\ensuremath{\ensuremath{\mathitbf{p}}}',\ensuremath{\ensuremath{\mathitbf{p}}})$ is the transition rate from $\ensuremath{\ensuremath{\mathitbf{p}}}'$ to $\ensuremath {\ensuremath {\mathitbf {p}}}$ . The sum is performed over all states available for scattering to and from $\ensuremath {\ensuremath {\mathitbf {p}}}$ . Physically speaking, the collision term incorporates the interaction of the carriers with the lattice (phonon scattering), the influence of ionized impurities, as well as additional scattering caused by inhomogeneities in the grid in material alloys and has to be modeled accordingly [65,74].

An alternative approach for the derivation of the Boltzmann transport equation can be found e.g. in [73], which is also useful for solving it with the help of path integrals. The motion of free carriers is influenced by an external electric field and the resulting path through $(\ensuremath{\ensuremath{\mathitbf{r}}},\ensuremath{\ensuremath{\mathitbf{k}}})$ -space is described with trajectories following Newton's laws. Scattering events cause the particle to change its momentum, but not its position.

M. Wagner: Simulation of Thermoelectric Devices