3.5.10 Electrothermal Transport Model

For the simulation of thermoelectric devices, it is important to accurately describe the energy relations within the device. In the electrothermal transport model, the contributions of the carrier subsystems and the lattice are combined to one heat-flux equation, whereby a rigorous treatment of the coupling mechanisms between the thermal and the electrical description is achieved.

Since the driving forces within thermoelectric devices are very low compared to modern CMOS devices, the carrier gas can be safely assumed to be in local thermodynamic equilibrium with the lattice. Thus, the inclusion of additional equations accounting for carriers driven far from equilibrium to the constituent equation system are an unnecessary computational overhead. Assuming local thermodynamic equilibrium, the electrothermal transport model can be obtained from the energy transport model as a starting point.

Besides Poisson's equation, the electrothermal transport model incorporates carrier balance equations as well as current equations for both electrons and holes. The energy relations are described by an additional heat-flow equation, which is accessible from both a systematic and a phenomenological point of view.

In the sequel, the electrothermal transport model is governed based on the moment equations derived by Bløtekjær's approach. The calculation with Stratton's equations is similar, and includes additional terms accounting for the scattering parameters ${\ensuremath{r_\nu}}$ . The energy flux equation derived after Bløtekjær (3.122) assuming local thermal equilibrium expressed in terms of the particle flux reads

$$\ensuremath{\ensuremath{\mathitbf{j}}_\nu^\mathrm{u}}= \ensuremat... ...}}}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}$$ (3.149)

with the thermal conductivity $\ensuremath{\ensuremath{\kappa_{\ensuremath{\nu}}}}$ of the carrier subsystem obeying a Wiedemann-Franz law

$$\ensuremath{\ensuremath{\kappa_{\ensuremath{\nu}}}}= \frac{5}{2} ... ...} \ensuremath{\ensuremath{\mu}_\nu^\mathrm{u}}\ensuremath{\nu}\ensuremath{T}\,.$$ (3.150)

In (3.149), the two contributions to the energy flux by a moving carrier gas as well as heat conduction by the carrier gas can be identified. However, in non-degenerate semiconductors, the thermal conductivities of the carrier subsystems can be neglected against the lattice contribution [95]. Insertion of (3.149) into the energy balance equation (3.65) yields

$$\ensuremath{\ensuremath{\partial_{t} \ensuremath{w}}} + \ensurema... ...remath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T} \right)$$ (3.151)

$$+ \ensuremath{\mathrm{s}_\nu}\mathrm{q}\ensuremath{\ensuremath{\m... ...nsuremath{\tilde{\varphi}} - \ensuremath{G_\nu^\ensuremath{\mathcal{E}}}= 0 \,.$$

In order to obtain expressions accessible by physical interpretation, a few rearrangements have to be performed on (3.151). First, the gradient of the electrochemical potential has to be substituted by the current relation (3.88)

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\en... ...\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\,.$$ (3.152)

Furthermore, the Seebeck coefficient

$$\ensuremath{\ensuremath{\alpha}_{\ensuremath{\nu}}}= \ensuremath{... ...ac{5}{2} - \ln \frac{\ensuremath{\nu}}{\ensuremath{N_\mathrm{c,v}}} \right) \,,$$ (3.153)

is introduced which is described closer in Section 3.5.12. Inserting (3.152) and (3.153) to (3.151) yields

$$\ensuremath{\ensuremath{\partial_{t} \frac}}{3}{2} k_\ensuremath{... ...h{\mathitbf{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{\nu}}}$$ (3.154)

$$- \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\nu^\mathrm{u}}}... ...nsuremath{\tilde{\varphi}} - \ensuremath{G_\nu^\ensuremath{\mathcal{E}}}= 0 \,.$$

Equation (3.154) denotes the energy balance equation for the electron and hole subsystem, respectively. The lattice contribution incorporates an additional heat flux term, which is the dominant contribution to heat conduction within most moderately doped semiconductors. This heat flux is expressed by a Fourier law with the according lattice heat conductivity $\ensuremath{\kappa_{\mathrm{L}}}$ . The energy balance equations for the three subsystems read

$$%electrons \frac{3}{2} k_\ensuremath{\mathrm{B}}\ensuremath{\ensu... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{n}}$$ (3.155)

$$\quad + \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\ensuremat... ...remath{\tilde{\varphi}}+ \ensuremath{G_\ensuremath{n}^\ensuremath{\mathcal{E}}}$$

$$%holes \frac{3}{2} k_\ensuremath{\mathrm{B}}\ensuremath{\ensurema... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{p}}$$ (3.156)

$$\quad - \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\ensuremat... ...remath{\tilde{\varphi}}+ \ensuremath{G_\ensuremath{p}^\ensuremath{\mathcal{E}}}$$

$$%lattice \ensuremath{c_{\mathrm{L}}}\ensuremath{\ensuremath{\part... ...uremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\right)$$ (3.157)

The final heat-flow equation is governed as the sum of the contributions of all three subsystems. Both specific heat and thermal conductivity are expressed as parameters for the entire semiconductor. Thus, the heat-flow equation reads

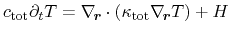$$\ensuremath{c_{\mathrm{tot}}}\ensuremath{\ensuremath{\partial_{t}... ...th{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\right) + \ensuremath{H}$$ (3.158)

with the heat source term

$$\ensuremath{H}= \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\e... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.159)

$$\quad + \ensuremath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}\ensuremath{R}$$

$$\quad + \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\ensuremat... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{n}}$$

$$\quad - \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\ensuremat... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{p}}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\frac{\ensurem... ...thitbf{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}}\right)$$

$$\quad + \mathrm{q}\left( \left( 1 - \ensuremath{\frac{\ensuremath... ...nsuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{\tilde{\varphi}}\,.$$

For the stationary case, the divergence terms of the electron and hole currents can be expressed by the net recombination rate due to the vanishing $\ensuremath{\ensuremath{\partial_{t} \ensuremath{\nu}}}$ -term in the carrier balance equation (3.37). For this special case, the heat source term becomes

$$\ensuremath{H}= \ensuremath{\frac{\ensuremath{\ensuremath{\mu}_\e... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.160)

$$\quad + \mathrm{q}\left( \ensuremath{\frac{\ensuremath{\ensuremat... ...emath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}\right) \ensuremath{G}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\frac{\ensurem... ...thitbf{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}}\right)$$

$$\quad + \mathrm{q}\left( \left( 1 - \ensuremath{\frac{\ensuremath... ...nsuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{\tilde{\varphi}}\,.$$

An often used, but not fully justifiable assumption is that the mobility ratios equal unity for each electrons and holes [86]. Therefore, the heat source term reduces to

$$\ensuremath{H}= \mathrm{q}\frac{\ensuremath{\left\vert \ensuremat... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.161)

$$\quad + \mathrm{q}\left( \ensuremath{T}\left( \ensuremath{\ensure... ...emath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}\right) \ensuremath{G}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\ensuremath{\m... ...f{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}} \right) \,.$$

The contributions to equation (3.161) are the Joule heat losses due to current flow throughout the structure, the recombination heat, which is transferred to the lattice due to carrier recombination, and the Thomson heat. This expression is compatible to an approach based on considerations of phenomenological irreversible thermodynamics, which is summarized in the following section.

M. Wagner: Simulation of Thermoelectric Devices