3.5.11 Phenomenological Approach

Besides the systematic approach carried out in the preceding sections, the thermoelectric behavior of semiconductors can also be explained by an approach based on phenomenological irreversible thermodynamics [54,96].

For the non-isothermal case, besides the gradient of the electrochemical potential a temperature gradient yields an additional driving force which is known as the Seebeck effect in the particle current relations

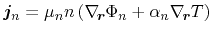$$\ensuremath{\ensuremath{\mathitbf{j}}_{n}}= \ensuremath{\ensurema... ...uremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\right)$$ (3.162)

$$\ensuremath{\ensuremath{\mathitbf{j}}_{p}}= - \ensuremath{\ensure... ...ath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\right) \,,$$ (3.163)

which are similar to the systematically derived equations. The corresponding heat fluxes are identified as

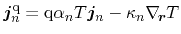$$\ensuremath{\ensuremath{\mathitbf{j}}_{n}^\mathrm{q}}= \mathrm{q}... ...}}}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}$$ (3.164)

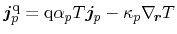$$\ensuremath{\ensuremath{\mathitbf{j}}_{p}^\mathrm{q}}= \mathrm{q}... ...}}}\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}$$ (3.165)

by the application of Onsager's reciprocity theorem. The total energy flux of all three subsystems is written as

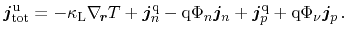$$\ensuremath{\ensuremath{\mathitbf{j}}_\mathrm{tot}^\mathrm{u}}= -... ...suremath{\Phi}_{\ensuremath{\nu}}}\ensuremath{\ensuremath{\mathitbf{j}}_{p}}\,.$$ (3.166)

The differential energy densities of electrons and holes are derived using Maxwell's relations [9] as

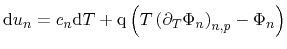$$\ensuremath{\mathrm{d}}\ensuremath{u_\ensuremath{n}}= \ensuremath... ...math{n},\ensuremath{p}}- \ensuremath{\ensuremath{\Phi}_{\ensuremath{n}}}\right)$$ (3.167)

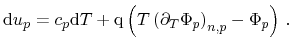$$\ensuremath{\mathrm{d}}\ensuremath{u_\ensuremath{p}}= \ensuremath... ...{n},\ensuremath{p}}- \ensuremath{\ensuremath{\Phi}_{\ensuremath{p}}}\right) \,.$$ (3.168)

Inserting the accumulated differential energy densities for the electron, hole, and lattice subsystems into the energy balance equation

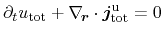$$\ensuremath{\ensuremath{\partial_{t} \ensuremath{u_\mathrm{tot}}}... ...remath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_\mathrm{tot}^\mathrm{u}}= 0$$ (3.169)

yields the heat conduction equation

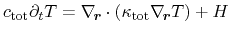$$\ensuremath{c_{\mathrm{tot}}}\ensuremath{\ensuremath{\partial_{t}... ...th{\ensuremath{\mathitbf{\nabla_{\!r}}}}}\ensuremath{T}\right) + \ensuremath{H}$$ (3.170)

accounting for the conservation of total energy with the heat source term

$$\ensuremath{H}= \mathrm{q}\frac{\ensuremath{\left\vert \ensuremat... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.171)

$$\quad + \mathrm{q}\left( \ensuremath{T}\left( \ensuremath{\partia... ...ath{p}} + \ensuremath{\ensuremath{\Phi}_{\ensuremath{p}}}\right) \ensuremath{G}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \left( \ensuremath{\partia... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{p}}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\ensuremath{\m... ...f{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}} \right) \,.$$

With the electrochemical potential (3.88) and the Seebeck coefficient (3.153) for Maxwell-Boltzmann statistics, the heat-source term can be rewritten to

$$\ensuremath{H}= \mathrm{q}\frac{\ensuremath{\left\vert \ensuremat... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.172)

$$\quad + \left( \frac{5}{2} k_\ensuremath{\mathrm{B}}\ensuremath{T}\right) \ensuremath{R}$$

$$\quad + \mathrm{q}\left( \ensuremath{\ensuremath{\alpha}_{\ensure... ...bf{\nabla_{\!r}}}}\ensuremath{\cdot}}\ensuremath{\ensuremath{\mathitbf{j}}_{p}}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\ensuremath{\m... ...tbf{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}}\right)\,,$$

which can be finally simplified for the static case because of the vanishing $\ensuremath{\ensuremath{\partial_{t} \ensuremath{\nu}}}$ -term in (3.37) to

$$\ensuremath{H}= \mathrm{q}\frac{\ensuremath{\left\vert \ensuremat... ...} \right\vert}^2}{\ensuremath{\ensuremath{\mu}_{\ensuremath{p}}}\ensuremath{p}}$$ (3.173)

$$\quad + \mathrm{q}\left( \ensuremath{T}\left( \ensuremath{\ensure... ...emath{\ensuremath{\mathcal{E}}_{\ensuremath{\mathrm{g}}}}\right) \ensuremath{G}$$

$$\quad + \mathrm{q}\ensuremath{T}\left( \ensuremath{\ensuremath{\m... ...f{\nabla_{\!r}}}}}\ensuremath{\ensuremath{\alpha}_{\ensuremath{p}}} \right) \,.$$

The final result is equal to the heat-source term of the systematically derived heat-flow equation in Section 3.5.10 under several simplifying assumptions, when the electrochemical potential as well as the Seebeck coefficient are expressed by the corresponding relations for Maxwell-Boltzmann statistics.

M. Wagner: Simulation of Thermoelectric Devices