The specific heat capacity
 enters the heat flux equation as a time
independent model parameter and is defined as the energy per mass needed to
increase the temperature of a specimen by one Kelvin. It is modeled by
[209]
enters the heat flux equation as a time
independent model parameter and is defined as the energy per mass needed to
increase the temperature of a specimen by one Kelvin. It is modeled by
[209]
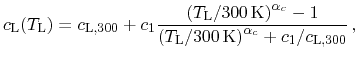 |
(5.13) |
where
 is the specific heat capacity at
is the specific heat capacity at
 .
Fig. 5.2 shows the temperature dependence of the specific heat
capacities for PbTe and SnTe, respectively. Measurement data have been
obtained from [210,174,211,121,212]
for lead telluride and from [213,214] for tin telluride, where
the latter is a review of several collected papers. For the ternary alloys
Pb
.
Fig. 5.2 shows the temperature dependence of the specific heat
capacities for PbTe and SnTe, respectively. Measurement data have been
obtained from [210,174,211,121,212]
for lead telluride and from [213,214] for tin telluride, where
the latter is a review of several collected papers. For the ternary alloys
Pb Sn
Sn Te, the resulting specific heat capacity is expressed as a
linear interpolation between the values for the according pure materials
Te, the resulting specific heat capacity is expressed as a
linear interpolation between the values for the according pure materials
 |
(5.14) |
where A stands for lead telluride, B for tin telluride and  denotes the
according atomistic content.
denotes the
according atomistic content.
Table 5.5:
Parameters for the specific heat capacity models for PbTe and SnTe.
|
|
Figure 5.2:
Temperature dependence of the specific heat capacity of lead
telluride and tin telluride including measurement data and model parameter
sets.
|
![\includegraphics[width=10cm]{figures/materials/PbTe/spec_heat2.eps}](img665.png) |
M. Wagner: Simulation of Thermoelectric Devices
![]() enters the heat flux equation as a time
independent model parameter and is defined as the energy per mass needed to
increase the temperature of a specimen by one Kelvin. It is modeled by
[209]
enters the heat flux equation as a time
independent model parameter and is defined as the energy per mass needed to
increase the temperature of a specimen by one Kelvin. It is modeled by
[209]
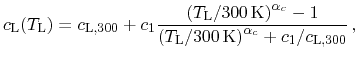
![\includegraphics[width=10cm]{figures/materials/PbTe/spec_heat2.eps}](img665.png)