The thermal conductivity  parametrizes the flux term in the heat flux
equation and depicts the energy flux per area and temperature difference
transported within a homogeneous material. Measurement of the thermal
conductivity is conventionally based on gathering the temperature difference
caused by a steady heat flow, but also more sophisticated approaches like the
parametrizes the flux term in the heat flux
equation and depicts the energy flux per area and temperature difference
transported within a homogeneous material. Measurement of the thermal
conductivity is conventionally based on gathering the temperature difference
caused by a steady heat flow, but also more sophisticated approaches like the
 -method can be applied in special cases [215]. The total
thermal conductivity in semiconductors consists of the lattice and the
electronic contribution, which is connected to the electrical conductivity by a
Wiedemann-Franz law. While the lattice thermal conductivity, which is the
dominant mechanism over a wide range of carrier concentrations in silicon,
germanium, and several III-V semiconductors, is commonly modeled as a
temperature dependent power law [133], the electron or hole
contribution in n- and p-type materials gains weight in heavily doped samples.
In the intrinsic range, both electrons and holes contribute to the thermal
conductivity, which is referred to as the bipolar contribution. In lead
telluride, these additional contributions to the thermal conductivity caused
by the carrier gas play already a significant role at technically relevant
carrier concentrations [121]. Based on the theoretical
considerations presented in [125], the thermal conductivity
dependence on the temperature and the electron concentration can be modeled as
-method can be applied in special cases [215]. The total
thermal conductivity in semiconductors consists of the lattice and the
electronic contribution, which is connected to the electrical conductivity by a
Wiedemann-Franz law. While the lattice thermal conductivity, which is the
dominant mechanism over a wide range of carrier concentrations in silicon,
germanium, and several III-V semiconductors, is commonly modeled as a
temperature dependent power law [133], the electron or hole
contribution in n- and p-type materials gains weight in heavily doped samples.
In the intrinsic range, both electrons and holes contribute to the thermal
conductivity, which is referred to as the bipolar contribution. In lead
telluride, these additional contributions to the thermal conductivity caused
by the carrier gas play already a significant role at technically relevant
carrier concentrations [121]. Based on the theoretical
considerations presented in [125], the thermal conductivity
dependence on the temperature and the electron concentration can be modeled as
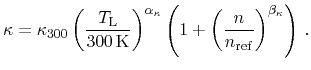 |
(5.15) |
The according parameters are collected in Table 5.6.
Table 5.6:
Parameter values for the lead telluride thermal conductivity model
incorporating the carrier contribution.
|
|
In Fig. 5.3, the agreement between Bhandari's data
[125] and the model is illustrated. Several measurement data
available in literature [216,217,218,219] show a
general decrease of the thermal conductivity for increasing temperatures with
an alleviated or even reverse trend at higher temperatures caused by the
increased electronic contribution due to additionally available free carriers.
Figure 5.3:
Dependence of the thermal conductivity of lead telluride on the
lattice temperature and carrier concentration. While red glyphs depict Bhandari's
data [125], the surface denotes the modeled thermal
conductivity.
|
![\includegraphics[width=10cm]{figures/materials/PbTe/therm_cond.eps}](img676.png) |
The heat flux between two points with temperatures
 and
and
 is
calculated by the integral
is
calculated by the integral
 |
(5.16) |
assuming the carrier concentration to be constant throughout the discretization
box.
In Pb Sn
Sn Te, alloy scattering enters as an additional mechanism and
thus the thermal conductivity is drastically reduced compared to pure PbTe and
SnTe. Fig. 5.4 depicts the variation of the thermal
conductivity with respect to the material composition at
Te, alloy scattering enters as an additional mechanism and
thus the thermal conductivity is drastically reduced compared to pure PbTe and
SnTe. Fig. 5.4 depicts the variation of the thermal
conductivity with respect to the material composition at
 .
Measurement data have been collected from
[220,221,222], where the latter two comprise
investigations of sintered samples which explains the lower thermal
conductivity values. The lattice component has been theoretically investigated
by molecular-dynamics studies in [223] and by subtracting the
electronic contribution
.
Measurement data have been collected from
[220,221,222], where the latter two comprise
investigations of sintered samples which explains the lower thermal
conductivity values. The lattice component has been theoretically investigated
by molecular-dynamics studies in [223] and by subtracting the
electronic contribution
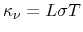 |
(5.17) |
derived from the electron conductivity  , the Lorentz number
, the Lorentz number  and
the temperature [220]. The model for the material composition
dependent thermal conductivity in alloys reads [133]
and
the temperature [220]. The model for the material composition
dependent thermal conductivity in alloys reads [133]
where  and
and  denote the SnTe and PbTe content, respectively.
denote the SnTe and PbTe content, respectively.
 is the thermal conductivity for PbTe at room temperature,
is the thermal conductivity for PbTe at room temperature,
 analogously for SnTe, and
analogously for SnTe, and  the bowing factor accounting for the alloy
scattering reduction of the thermal conductivity. The exponents describing the
temperature dependence are interpolated linearly between the values for the
pure material constituents.
The additional electronic contribution can be estimated by
the bowing factor accounting for the alloy
scattering reduction of the thermal conductivity. The exponents describing the
temperature dependence are interpolated linearly between the values for the
pure material constituents.
The additional electronic contribution can be estimated by
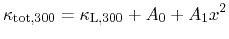 |
(5.20) |
for Pb Sn
Sn Te based on the data published in [220].
According values for the temperature exponents
Te based on the data published in [220].
According values for the temperature exponents
 and
and
 have been identified for the lattice thermal conductivity
based on data published in [222] and [224]. The
parameters for the material composition dependent thermal conductivity model
are collected in Table 5.7.
have been identified for the lattice thermal conductivity
based on data published in [222] and [224]. The
parameters for the material composition dependent thermal conductivity model
are collected in Table 5.7.
Table 5.7:
Parameter values for the material composition dependent PbSnTe thermal conductivity models.
|
|
A decrease of the thermal conductivity compared to single crystals due to grain
boundary scattering in sintered materials has been reported in
[124,126,225] to be as high as  in pure lead
telluride and
in pure lead
telluride and  in disordered lead telluride alloys. However, a
drastic decrease of the thermal conductivity is reported in [128]
for grain sizes in the range of
in disordered lead telluride alloys. However, a
drastic decrease of the thermal conductivity is reported in [128]
for grain sizes in the range of
 . Furthermore, the
influence of the grain size within sintered
. Furthermore, the
influence of the grain size within sintered
 is investigated in
[127] for hot and cold pressed materials. Recent work has dealt with
the dependence of the thermal conductivity on the pressure during fabrication
using high temperature and high pressure processes [226,227].
is investigated in
[127] for hot and cold pressed materials. Recent work has dealt with
the dependence of the thermal conductivity on the pressure during fabrication
using high temperature and high pressure processes [226,227].
M. Wagner: Simulation of Thermoelectric Devices
![]() parametrizes the flux term in the heat flux
equation and depicts the energy flux per area and temperature difference
transported within a homogeneous material. Measurement of the thermal
conductivity is conventionally based on gathering the temperature difference
caused by a steady heat flow, but also more sophisticated approaches like the
parametrizes the flux term in the heat flux
equation and depicts the energy flux per area and temperature difference
transported within a homogeneous material. Measurement of the thermal
conductivity is conventionally based on gathering the temperature difference
caused by a steady heat flow, but also more sophisticated approaches like the
![]() -method can be applied in special cases [215]. The total
thermal conductivity in semiconductors consists of the lattice and the
electronic contribution, which is connected to the electrical conductivity by a
Wiedemann-Franz law. While the lattice thermal conductivity, which is the
dominant mechanism over a wide range of carrier concentrations in silicon,
germanium, and several III-V semiconductors, is commonly modeled as a
temperature dependent power law [133], the electron or hole
contribution in n- and p-type materials gains weight in heavily doped samples.
In the intrinsic range, both electrons and holes contribute to the thermal
conductivity, which is referred to as the bipolar contribution. In lead
telluride, these additional contributions to the thermal conductivity caused
by the carrier gas play already a significant role at technically relevant
carrier concentrations [121]. Based on the theoretical
considerations presented in [125], the thermal conductivity
dependence on the temperature and the electron concentration can be modeled as
-method can be applied in special cases [215]. The total
thermal conductivity in semiconductors consists of the lattice and the
electronic contribution, which is connected to the electrical conductivity by a
Wiedemann-Franz law. While the lattice thermal conductivity, which is the
dominant mechanism over a wide range of carrier concentrations in silicon,
germanium, and several III-V semiconductors, is commonly modeled as a
temperature dependent power law [133], the electron or hole
contribution in n- and p-type materials gains weight in heavily doped samples.
In the intrinsic range, both electrons and holes contribute to the thermal
conductivity, which is referred to as the bipolar contribution. In lead
telluride, these additional contributions to the thermal conductivity caused
by the carrier gas play already a significant role at technically relevant
carrier concentrations [121]. Based on the theoretical
considerations presented in [125], the thermal conductivity
dependence on the temperature and the electron concentration can be modeled as
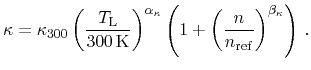
![\includegraphics[width=10cm]{figures/materials/PbTe/therm_cond.eps}](img676.png)
![]() and
and
![]() is
calculated by the integral
is
calculated by the integral

![\includegraphics[width=10cm]{figures/materials/PbTe/therm_cond_PbSnTe.eps}](img680.png)
![]() Sn
Sn![]() Te, alloy scattering enters as an additional mechanism and
thus the thermal conductivity is drastically reduced compared to pure PbTe and
SnTe. Fig. 5.4 depicts the variation of the thermal
conductivity with respect to the material composition at
Te, alloy scattering enters as an additional mechanism and
thus the thermal conductivity is drastically reduced compared to pure PbTe and
SnTe. Fig. 5.4 depicts the variation of the thermal
conductivity with respect to the material composition at
![]() .
Measurement data have been collected from
[220,221,222], where the latter two comprise
investigations of sintered samples which explains the lower thermal
conductivity values. The lattice component has been theoretically investigated
by molecular-dynamics studies in [223] and by subtracting the
electronic contribution
.
Measurement data have been collected from
[220,221,222], where the latter two comprise
investigations of sintered samples which explains the lower thermal
conductivity values. The lattice component has been theoretically investigated
by molecular-dynamics studies in [223] and by subtracting the
electronic contribution

![]() in pure lead
telluride and
in pure lead
telluride and ![]() in disordered lead telluride alloys. However, a
drastic decrease of the thermal conductivity is reported in [128]
for grain sizes in the range of
in disordered lead telluride alloys. However, a
drastic decrease of the thermal conductivity is reported in [128]
for grain sizes in the range of
![]() . Furthermore, the
influence of the grain size within sintered
. Furthermore, the
influence of the grain size within sintered
![]() is investigated in
[127] for hot and cold pressed materials. Recent work has dealt with
the dependence of the thermal conductivity on the pressure during fabrication
using high temperature and high pressure processes [226,227].
is investigated in
[127] for hot and cold pressed materials. Recent work has dealt with
the dependence of the thermal conductivity on the pressure during fabrication
using high temperature and high pressure processes [226,227].