3.2.2 Anisotropic Diffusivity: Diffusion Dependence on Stress

Residual mechanical stresses are introduced on interconnect lines as a result of the fabrication process flow [141]. These stresses can be very high, significantly affecting the diffusion coefficient of the interconnect metal atoms [142].

Typically, the diffusion dependence on stress is taken into account through a simple modification of the usual diffusion coefficient expression (2.10) to [54,97]

$$D(\symHydStress)=D_0\exp\left(\frac{-\Ea + \symAtomVol\symHydStress}{\kB\T}\right).$$ (3.13)

In this way, (3.13) describes the effect of a scalar hydrostatic stress on the scalar diffusion coefficient. However, Flynn [143] pointed out that, for a homogeneously deformed cubic crystal with strain field $\symStrain_{kl}$, there is an additional contribution proportional to $\symStrain_{kl}$ to the diffusion of the form

$$D_{ij} = D(0)\symKronecker + \sum_{kl}d_{ijkl}\symStrain_{kl},$$ (3.14)

where $d_{ijkl}$ is the elastodiffusion tensor, which can be experimentally determined. Here, the simple scalar diffusivity is replaced by a tensorial quantity. Consequently, in the presence of a stress field the diffusivity can now become anisotropic, depending on the properties of $d_{ijkl}$.

Based on microscopic lattice theory, Dederichs and Schroeder [142] showed that the diffusivity in a simple face-centered cubic crystal (fcc) follows

$$D_{ij} = \frac{1}{2}\sum_{h} R_i^h R_j^h \Gamma^h,$$ (3.15)

where $\vec R^h$ is the jump vector for a hop $h$ and $\Gamma^h$ is the corresponding jump rate. From classical thermodynamics the jump rate is given by [59,144]

$$\Gamma^h = \nu\exp\left[-\frac{E_m^h(\boldsymbol\symStrain)}{\kB\T}\right],$$ (3.16)

where $\nu$ is the Debye frequency ( $\sim 10^{13}$ s$^{-1}$ for metals [144]) and $E_m^h$ is the migration energy barrier. The presence of an external strain field affects the jump rate by changing the migration energy barrier according to [145]

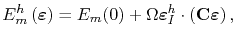$$E_m^h\left(\boldsymbol\symStrain\right) = E_m(0) + \symAtomVol\bo... ...\symStrain_I^{h}\ensuremath{\cdot}\left(\mathbf{C}\boldsymbol\symStrain\right),$$ (3.17)

where $E_m(0)$ is the migration energy barrier in the absence of an external field, $\boldsymbol\symStrain_I^{h}$ is the induced strain, $\mathbf{C}$ is the elasticity tensor, and $\boldsymbol\symStrain$ is the applied external strain. For a fcc crystal the elasticity tensor has the form [146]

$$\mathbf{C}= \begin{bmatrix}C_{11} &C_{12} &C_{12} &0 &0 &0 \\ C_{... ... &C_{44} &0 &0 \\ 0 &0 &0 &0 &C_{44} &0 \\ 0 &0 &0 &0 &0 &C_{44} \end{bmatrix}.$$ (3.18)

Combining (3.16) and (3.17) one obtains

$$\Gamma^h = \Gamma_0\exp\left[-\frac{\symAtomVol\boldsymbol\symStr... ...}\ensuremath{\cdot}\left(\mathbf{C}\boldsymbol\symStrain\right)}{\kB\T}\right],$$ (3.19)

with

$$\Gamma_0 = \nu\exp\left[-\frac{E_m(0)}{\kB\T}\right].$$ (3.20)

Considering a single vacant point defect in a crystal lattice, the local volumetric strain induced by the presence of this vacancy is given by

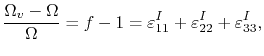$$\frac{\symVacVol - \symAtomVol}{\symAtomVol} = \symVacRelFactor-1 = \symStrain_{11}^I + \symStrain_{22}^I + \symStrain_{33}^I,$$ (3.21)

where $\symVacVol$ is the vacancy volume and $\symStrain_{11}^I$, $\symStrain_{22}^I$, and $\symStrain_{33}^I$ are the induced strains in the given directions. Due to the symmetry of a vacant point defect

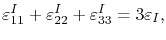$$\symStrain_{11}^I + \symStrain_{22}^I + \symStrain_{33}^I = 3\symStrain_I,$$ (3.22)

which together with (3.21) yields

$$\symStrain_I = -\frac{1-\symVacRelFactor}{3}.$$ (3.23)

Thus, the induced strain tensor becomes

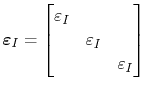$$\boldsymbol\symStrain_I=\begin{bmatrix}\symStrain_I & &\\ & \symStrain_I &\\ & & \symStrain_I\end{bmatrix}$$ (3.24)

and the induced strain vector is determined by

$$\boldsymbol\symStrain_I^{h} = \vert\boldsymbol\symStrain_I\ensuremath{\cdot}\vec{r}_h\vert,$$ (3.25)

where $\vec{r}_h$ is a jump unit vector for a hop $h$.

Normalizing (3.15) with the jump distance $\lambda$ and summing over the $z$ nearest neighbors ($z=12$ for fcc crystals) one obtains

$$D_{ij} = \frac{1}{2}\lambda^2\sum_{h=1}^{z} \frac{R_i^h}{\lambda}... ...h}{\lambda} \Gamma^h = \frac{1}{2}\lambda^2\sum_{h=1}^{z} r_i^h r_j^h \Gamma^h.$$ (3.26)

Substituting (3.19) in this equation, the diffusivity tensor in the presence of a external stress field is determined through the expression

$$D_{ij} = \frac{3}{Z}D_0\sum_{h=1}^{z} r_i^h r_j^h \exp\left[-\fra... ...}\ensuremath{\cdot}\left(\mathbf{C}\boldsymbol\symStrain\right)}{\kB\T}\right],$$ (3.27)

where $D_0$ is given by [144]

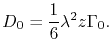$$D_0 = \frac{1}{6}\lambda^2z\Gamma_0.$$ (3.28)

In order to take into account the anisotropy of diffusion, the scalar diffusivity, $\DV$, in the flux equation (3.9) is replaced by the stress dependent diffusivity tensor $\mathbf{D}$ yielding

$$\vec\JV = -\mathbf{D} \biggl(\ensuremath{\nabla{\CV}} + \frac{\ve... ...symVacRelFactor\symAtomVol}{\kB\T}\CV\ensuremath{\nabla{\symHydStress}}\biggr),$$ (3.29)

with $\mathbf{D}$ calculated via (3.27). In this way, the development of mechanical stress can lead to anisotropic diffusion in the interconnect line, therefore, affecting the material transport along the line under electromigration.