



Next: 3.1.4 The Lattice Heat
Up: 3.1 Sets of Partial
Previous: 3.1.2 The Drift-Diffusion Transport
In the hydrodynamic transport model,
carrier temperatures are allowed to be different from the lattice temperature.
The basic equations (3.1) through
(3.3) are augmented by energy balance equations which
determine the carrier temperatures. The current relations take the form
| |
|
 |
(3.6) |
| |
|
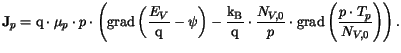 |
(3.7) |
The energy balance equations state conservation
of the average carrier energies. In terms of the carrier temperatures  and
and  they can be written as
they can be written as
| |
|
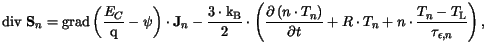 |
(3.8) |
| |
|
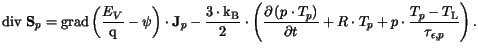 |
(3.9) |
Here,
 and
and
 denote the energy relaxation times, while
denote the energy relaxation times, while
 and
and  are the energy fluxes.
are the energy fluxes.
| |
|
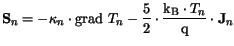 |
(3.10) |
| |
|
 |
(3.11) |
The carrier thermal conductivities,  and
and
 , are assumed to obey a generalized Wiedemann-Franz
law.
, are assumed to obey a generalized Wiedemann-Franz
law.
| |
|
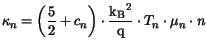 |
(3.12) |
| |
|
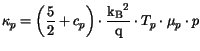 |
(3.13) |
The heat capacities  and
and  are usually neglected (
are usually neglected ( ).
).
Strictly speaking, the model described above in this subsection represents an energy
transport (ET) model. Such a model is obtained when in the course of deriving the
moment equations the average kinetic energy is consequently neglected against
the thermal energy, assuming that
 . Since in the literature the terms energy transport
and hydrodynamic transport are often used synonymously, and since during
the development of MINIMOS-NT the term hydrodynamic transport was used,
this notation is retained throughout this work.
. Since in the literature the terms energy transport
and hydrodynamic transport are often used synonymously, and since during
the development of MINIMOS-NT the term hydrodynamic transport was used,
this notation is retained throughout this work.




Next: 3.1.4 The Lattice Heat
Up: 3.1 Sets of Partial
Previous: 3.1.2 The Drift-Diffusion Transport
Vassil Palankovski
2001-02-28

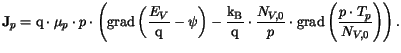
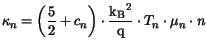
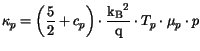
![]() . Since in the literature the terms energy transport
and hydrodynamic transport are often used synonymously, and since during
the development of MINIMOS-NT the term hydrodynamic transport was used,
this notation is retained throughout this work.
. Since in the literature the terms energy transport
and hydrodynamic transport are often used synonymously, and since during
the development of MINIMOS-NT the term hydrodynamic transport was used,
this notation is retained throughout this work.