



Next: B5. Gauß Function
Up: B. Optimization
Previous: B3. Two Norm
B4. Some Derivatives of Scalar Value Functions With Respect to a Vector
The first derivative of the scalar product of two Vectors  and
and
 is
is
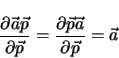 |
(B6) |
if vector  is independent of
is independent of  .
.
The derivative of the matrix built by the product of
 is
is
 |
(B7) |
if the matrix  is quadratic and independent of
is quadratic and independent of  .
.
R. Plasun
![]() and
and
![]() is
is
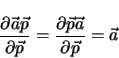
![]() is
is
