5.3 Validation of the trace introduction by HFSS^® simulations

An empirical validation of the proposed trace introduction method with (5.6) and (5.9) is carried out by HFSS^® simulations. HFSS^® is a FEM based three-dimensional full wave simulation tool from Ansoft^® [76].
A first HFSS^® enclosure model with a trace, depicted in Figure 5.5(c), is simulated with ports at the source and the load positions of the trace and three measurement ports at the slot. In a second HFSS^® model, presented in Figure 5.5(d), the trace is removed and ports are defined between the bottom and the cover plane of the enclosure in the same positions as the trace load and source ports in the first model. The enclosure cover has been removed in Figure 5.5(c) and Figure 5.5(d) to enable a view of the inside. The enclosure with cover is depicted in Figure 5.5(b), and Figure 5.5(a) depicts the bounding box, with absorbing boundaries at the surface, that surrounds the enclosure in the simulation models. Lumped ports are defined in HFSS^® on rectangular surfaces which are small compared to the wavelength of the highest simulated frequency. HFSS^® calculates the S-parameter matrix of the ports, which is transformed to a Z-parameter matrix. Proven convergence of the HFSS^® simulation is given through a monotone decrease of S-parameter results differences from two consecutive adaptive mesh refinement iterations. For the model in Figure 5.5(c) the transfer impedance from the trace source port to a measurement port at the slot is

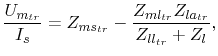$$\frac{U_{m_{tr}}}{I_{s}}=Z_{ms_{tr}}-\frac{Z_{ml_{tr}}Z_{la_{tr}}}{Z_{ll_{tr}}+Z_{l}},$$ (5.10)

where $Z_{ms_{tr}}$, $Z_{ml_{tr}}$ and $Z_{la_{tr}}$ are the Z-parameters of this HFSS^® model and $Z_{l}$ is an arbitrary trace load. HFSS^® would also enable the trace load in the model to be defined and the transfer impedance to, thus, be obtained directly instead of using (5.10). However, this would require one HFSS^® simulation for each load. Therefore, results for different loads are obtained efficiently by the described model which requires only one HFSS^® simulation. According to the described trace introduction method, the transfer impedance is also obtained with (5.6) and (5.9) and the Z-matrix (4.17) of the HFSS^® model in Figure 5.5(d). The characteristic impedance of the trace in (5.6) is calculated in accordance with [77]

$$Z_{w}=(60\Omega)\ln\left[\frac{f_{1}(w_{t}/d)}{w_{t}/d}+\sqrt{1+\left(\frac{2d}{w_{t}}\right)^2}\right],$$ (5.11)

and

$$f_{1}(w_{t}/d)=6+(2\pi-6)e^{-(\texttt{30.666}d/w_{t})^\texttt{0.7528}},$$ (5.12)

where $w_{t}$ is the trace width and $d$ is the trace height above the ground plane. Equation (5.11) with the adjustment function (5.12) approximates the exact conformal mapping solution from [78], [79], for the characteristic impedance of a thin sheet trace in air. The approximation uncertainty is below 0.03% for $w_{t}/d\leq$1000.
For the purpose of simulating traces on a real PCB, the dielectric material of the PCB has to be considered with appropriate formulations [77], [80]. A comparison of the transfer impedances from both models validates the trace introduction method without any further simplifications, as there would be, if the cavity model were to be used instead of HFSS^® simulation. For instance, the radiation from the open enclosure slot is considered by surrounding the enclosure with the boundary box in the HFSS^® model (Figure 5.5(a)).

(a) Enclosure model inside a bounding box.

(b) Enclosure model with cover.

(c) Model with a trace (cover removed).

(d) Model with ports (cover removed).

Figure 5.5: HFSS^® models for the validation of the trace introduction method.

Figure 5.6 depicts the results of the described transfer impedance comparison for a trace at position (x=67mm, y=50mm), the measurement port at position (x=67mm, y=104mm) and trace loads of 0 Ohm, 1e9 Ohm, and 50 Ohm. The trace length is l=5mm, the trace width is $w_{t}$=2mm, the trace height above ground is d=0.65mm, and the enclosure dimensions are (L=134mm, W=104mm, h=7mm). To cover the whole ground-plane area, comparisons from nine trace positions are collected in Appendix A.1.

Load: 0 Ohm, magnitude.

Load: 0 Ohm, phase angle.

Load: 1e9 Ohm, magnitude.

Load: 1e9 Ohm, phase angle.

Load: 50 Ohm, magnitude.

Load: 50 Ohm, phase angle.

Figure 5.6: Transfer impedance from the trace source current to the slot measurement port at (67mm,104mm). The trace is located at position (67mm,50mm) and the trace length is 5mm. Trace orientation in y-direction. Comparison of HFSS results from a model with a trace and the results obtained with (5.6), (5.9) and a HFSS model with ports.

More comparisons are presented for a variation of the enclosure height, for a variation of the trace height above the ground plane, and for parallel planes with four open edges in Appendix A.2. All comparisons show very good agreement, both in magnitude and phase. Thus, the proposed trace introduction method with the analytical coupling factor is generally sufficient for electromagnetic emission simulation.

C. Poschalko: The Simulation of Emission from Printed Circuit Boards under a Metallic Cover