1 Derivation of the cavity model with the separation method

7.1.1 Derivation of the cavity model with the separation method

Applying the method of Bernoulli [103], the homogenous part of (4.13) is expressed by

$\displaystyle \frac{1}{X(x)}\frac{\partial^{2}}{\partial x}X(x)+\frac{1}{Y(y)}\frac{\partial^{2}}{\partial y}Y(y)+k^2=0$ with $\displaystyle \qquad U(x,y)=X(x)Y(y),$

(7.1)

which enables separation to

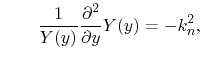$\displaystyle \frac{1}{X(x)}\frac{\partial^{2}}{\partial x}X(x)=-k_{m}^{2}$ and $\displaystyle \qquad\frac{1}{Y(y)}\frac{\partial^{2}}{\partial y}Y(y)=-k_{n}^{2},$

(7.2)

with

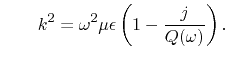$\displaystyle -k_{m}^{2}-k_{n}^{2}+k^{2}=0$ and $\displaystyle \qquad k^2=\omega^{2}\mu\epsilon\left(1-\frac{j}{Q(\omega)}\right).$

(7.3)

The general solution of these equations is

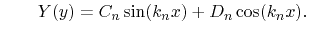$\displaystyle X(x)=A_{m}\sin(k_{m}x)+B_{m}\cos(k_{m}x)$ and $\displaystyle \qquad Y(y)=C_{n}\sin(k_{n}x)+D_{n}\cos(k_{n}x).$

(7.4)

The PMC boundary (4.16) on the open slot and the PEC boundaries (4.15) on the metallic walls according to Figure 7.1 are introduced by

$\begin{displaymath}\begin{array}[t]{ccc} &&\\ X(0)=X(L)=0&\Rightarrow&B_{m}=0... ...}}\quad\forall\quad n\in\mathbb{N}_{0}.\\ &&\\ \end{array}\end{displaymath}$

(7.5)

$k_{m}$ and $k_{n}$ are the eigenvalues of (4.13) for the rectangular enclosure in Figure 7.1. The fringing fields at the slot are considered by using the effective enclosure width $W_{e}=W+h/4$ instead of

. In [45] $W_{e}=W+h/2$ has been taken to consider the fringing fields for planes with two open boundaries associated with dimension

, but as the enclosure in Figure 7.1 has only one open edge, the correction must be performed by using $W_{e}=W+h/4$ . An additional correction has to be carried out to consider the wall thickness $d_{w}$ of the enclosure. This is not necessary in the case of power planes on a PCB, because the conducting layers are thin, although, a metallic enclosure usually has thicker walls. To consider a non-negligible wall thickness of the enclosure, the effective enclosure dimension in y-direction is

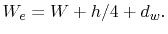$\displaystyle W_{e}=W+h/4+d_{w}.$

(7.6)

With (7.5) and (7.4) the solution of the homogenous part of (4.13) results in

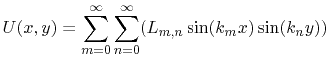$\displaystyle U(x,y)=\sum_{m=0}^{\infty}\sum_{n=0}^{\infty}(L_{m,n}\sin(k_{m}x)\sin(k_{n}y))$

(7.7)

$L_{m,n}$ are parameters which depend on the integer pair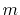

and

. These parameters are obtained by the following solution of (4.13). The port excitation with a current $I_{sp}$ on source point $(x_{sp},y_{sp})$ is expressed by

$\displaystyle J_{z}(x,y)=-I_{sp}\delta(x_{sp},y_{sp}),$

(7.8)

where $\delta(x_{sp},y_{sp})$ is the Dirac impulse. Consistency with standard voltage and current direction of the impedance matrix (4.17) is achieved with the negative sign. Inserting (7.7) and (7.8) into (4.13), multiplying with $\sin(k_{m1}x)\sin(k_{n1}y)$ and integrating over the area $(0\leq x\leq L,\, 0\leq y\leq W)$ yields

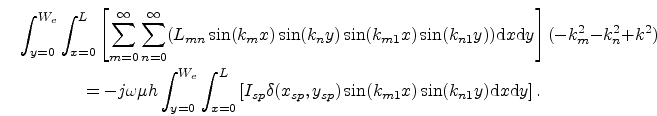$\displaystyle -j\omega\mu I_{sp}sin(k_{m1}x_{sp})\sin(k_{n1}y_{sp}).$

(7.9)

Where $m1\in \mathbb{N}_{0}$ and $n1\in \mathbb{N}_{0}$ . The right hand side of (7.9) becomes

$\displaystyle -j\omega\mu I_{sp}sin(k_{m1}x_{sp})\sin(k_{n1}y_{sp}).$

(7.10)

The left hand side of (7.9) vanishes for all $m\neq m1$ and also for all $n\neq n1$ according to the orthogonality of the base functions $\sin(k_{m}x)$ to $\sin(k_{m1}x)$ and $\sin(k_{n}y)$ to $\sin(k_{n1}y)$ , respectively. For

and

the left hand side integral solutions are

$\displaystyle \int_{x=0}^{L}\left[\sin^2(\frac{m\pi x}{L})\textrm{d}x\right]=\frac{L}{2},$

(7.11)

and

$\displaystyle \int_{x=0}^{W_{e}}\left[\sin^2(\frac{(2n+1)\pi x}{2W})\textrm{d}y\right]=\frac{W_{e}}{2}.$

(7.12)

Finally, the solution of (4.13) for the rectangular enclosure in Figure 7.1 becomes

$\displaystyle U(x,y)=\frac{j4\omega\mu hI_{sp}}{LW_{e}}\sum_{m=0}^{\infty}\sum_... ...}x_{sp})\sin(k_{n}y_{sp})\sin(k_{m}x)\sin(k_{n}y)}{k_{m}^2+k_{n}^2-k^2}\right].$

(7.13)

With (7.13) the coefficients of the impedance matrix (4.17) are

$\displaystyle Z_{ij}=\frac{j4\omega\mu h}{LW_{e}}\sum_{m=0}^{\infty}\sum_{n=0}^... ...)\sin(k_{n}y_{i})\sin(k_{m}x_{j})\sin(k_{n}y_{j})}{k_{m}^2+k_{n}^2-k^2}\right].$

(7.14)

The resonance frequencies of the enclosure obtained from the zeros of $k_{m}^2+k_{n}^2-k^2$ are

$\displaystyle f_{r}=\frac{c_{l}}{2\pi}\frac{1}{\sqrt{1-\frac{j}{Q(\omega)}}}\sq... ...i}\sqrt{\left(\frac{m\pi}{L}\right)^2+\left(\frac{(2n+1)\pi}{2W_{e}}\right)^2},$

(7.15)

where $c_{l}=1/\sqrt{\mu\epsilon}$ denotes the speed of light in the cavity.

C. Poschalko: The Simulation of Emission from Printed Circuit Boards under a Metallic Cover

			Dissertation Christian Poschalko
Previous: 7.1 Analytical cavity model for a rectangular enclosure Up: 7.1 Analytical cavity model for a rectangular enclosure Next: 7.1.2 Summary of the analytical cavity model of