2.5.2 Phonon Dispersion Relations of SW-CNTs

The phonon dispersion relations for a SW-CNT can be determined by folding that of a graphene layer (see Section 2.4.2). Since there are $2N$ carbon atoms in the unit cell of a CNT, $6N$ phonon dispersion branches for the three-dimensional vibrations of atoms are achieved. The corresponding one-dimensional phonon energy dispersion relation for the CNT is given by

$$\omega^{\mu\lambda}_{\mathrm{CNT}}(q) \ = \ \omega^{\lambda}_{\mathrm{g-2D}} (q\frac{{\bf K_2}}{\vert{\bf K_2}\vert}+\mu{\bf K_1})\ ,$$ (2.12)

where $\lambda=1,~\ldots,~6$ denotes the polarization, $\mu=0,\ldots,N-1$ is the azimuthal quantum number, and $-\pi/T<q\leq\pi/T$ is the wave-vector of phonons. However, the zone-folding method does not always give the correct dispersion relation for a CNT, especially in the low frequency region. For example, the out-of-plane tangential acoustic (ZA) modes of a graphene sheet do not give zero energy at the $q=0$ when rolled into a CNT. Here, at $q=0$, all the carbon atoms of the CNT move radially in and out-of-plane radial acoustic vibration, which corresponds to a breathing mode (RBM) with a non-zero frequency [37]. To avoid these difficulties, one can directly diagonalize the dynamical matrix (see Fig. 2.11-a).

Fundamental phonon polarizations in CNTs are radial (R), transverse (T), and longitudinal (L). As shown in Fig. 2.11-b, zone center phonons, also referred to as $\Gamma$-point phonons, can belong to the transverse acoustic (TA), the longitudinal acoustic (LA), the radial breathing mode (RBM), the out-of-plane optical branch (RO), the transverse optical (TO), or the longitudinal optical (LO) phonon branch. The LO phonon branch near the $\Gamma$-point has an energy of $\approx 190~\mathrm{eV}$, whereas the energy of the RBM phonon branch is inversely proportional to the CNT diameter

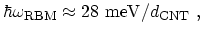$$\hbar\omega{_\mathrm{RBM}} \approx {28~\mathrm{meV}}/{d_\mathrm{CNT}} \ ,$$ (2.13)

where $d_\mathrm{CNT}$ is the diameter of the CNT in nanometer [41,42]. Zone boundary phonons, also referred to as $\mathrm{K}$-point phonons, are found to be a a mixture of fundamental polarizations [55].

Figure 2.11: The phonon dispersion relations of a) a $(10,10)$ armchair CNT [12] and b) a $(16,0)$ zigzag CNT with $\mu =0$, see (2.5.2) [55].

M. Pourfath: Numerical Study of Quantum Transport in Carbon Nanotube-Based Transistors