


Next: 3.3.1.2 Thermionic Field Emission
Up: 3.3.1 Semiconductor-Semiconductor Interfaces
Previous: 3.3.1 Semiconductor-Semiconductor Interfaces
The Continuous Quasi-Fermi level (CQFL) model assumes a constant Fermi level
over the interface during current flow. The relations for the current density  , the carrier concentration
, the carrier concentration  ,
the energy fluxes
,
the energy fluxes  , and the carrier temperatures
, and the carrier temperatures
 read as
follows:
read as
follows:
 |
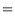 |
 |
(3.83) |
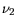 |
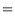 |
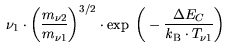 |
(3.84) |
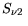 |
 |
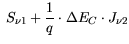 |
(3.85) |
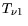 |
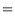 |
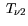 |
(3.86) |
The four equations constitute a Dirichlet boundary condition at the interface. The model
is mostly used to separate segments with no (homojunction) or little band gap
discontinuity relative to
 and the band gap. The higher the band gap discontinuity
and the band gap. The higher the band gap discontinuity
 , the
less appropriate the model. For heterojunctions the two models of the next section are to be used.
, the
less appropriate the model. For heterojunctions the two models of the next section are to be used.



Next: 3.3.1.2 Thermionic Field Emission
Up: 3.3.1 Semiconductor-Semiconductor Interfaces
Previous: 3.3.1 Semiconductor-Semiconductor Interfaces
Quay
2001-12-21
![]() , the carrier concentration
, the carrier concentration ![]() ,
the energy fluxes
,
the energy fluxes ![]() , and the carrier temperatures
, and the carrier temperatures
![]() read as
follows:
read as
follows: