3.3.4.2 The Ohmic Contact: Thermal Treatment

In an electro-thermal simulations two thermal boundary conditions can be applied. The first is the condition of a thermal resistance where the energy flux $\mathbf{S_n}$ through the Ohmic contact is determined using:

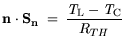$$\mathbf{n} \cdot \mathbf{S_n} = \frac{{\it T}_\mathrm{L}-{\it T}_\mathrm{C}}{R_{TH}}$$ (3.108)

i.e., the fluxes are proportional to the temperature gradient. $R_{TH}$ represents a global thermal resistance of materials surrounding the device, and ${\it T}_\mathrm{C}$ the contact temperature, i.e. the temperature of the heat reservoir assumed. If the thermal resistance $R_{TH}$ is set to zero, an isothermal boundary condition is applied:

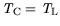$${\it T}_\mathrm{C}={\it T}_\mathrm{L}$$ (3.109)

For a macroscopic definition of $R_{TH}$, see Chapter 6. For the drift-diffusion transport model, similar to the semiconductor-semiconductor interface, the following entries are supplied:

$$\frac{\mathbf{J_n}}{q} \cdot \big( \Delta E_C + \varphi_m \big) + \frac{\mathbf{J_p}}{q}\cdot \big( \Delta E_V+ \varphi_m \big) = _{A} \mathbf{S_L}$$ (3.110)

For the hydrodynamic case the thermal heat flow is accounted for self-consistently.