

Next: 2.1.3 Segregation
Up: 2.1 Diffusion
Previous: 2.1.1 Extrinsic Dopant Diffusion
Today's commonly used models to describe diffusion phenomena are based
on the idea of pair-diffusion models, which do not only
describe the influence of charged dopants on each other but also the
reactions of dopants and the host lattice including its point defects.
At high temperatures native point defects are generated in the lattice of
a crystal. There are two point defects of interest for silicon:
- vacancies are defined as an empty lattice site
- interstitials are host atoms that reside in one of the
interstices of the lattice
These point defects lead to five different mechanisms of diffusion [Sze88][Fah89][Tay93]:
- direct mechanism: impurities with small atom-radii can move
directly between the host lattice as an interstitial.
- indirect mechanism: dopants with radii that are too
big for direct local exchanges can knock out lattice atoms and the so
widened gap offers foreign atoms the possibility to move through the
host lattice.
- exchange mechanism: a foreign atom that resides on a lattice
site (substitutional defect) can exchange its locality with
another substitutional defect. Because of the high invoked energy amount
this mechanism is negligible.
- ring mechanism: a more sophisticated exchange mechanism
occurs when a group of neighboring atoms exchange their sites
in a cyclic manner. This mechanism lacks of experimental verification.
- vacancy mechanism: a substitutional defect and a vacancy
building a pair are the means of mass transport trough the host
lattice.
Table 2.1 shows the experimentally verified reactions
of dopants for semiconductor manufacturing. In absence of the reaction
partner the dopants can not diffuse. That is why the damage of the
lattice as well as the process temperature have a significant effect
on the final doping distribution. In Chapter 4 a
five species phosphorus diffusion model will be discussed in detail.
Besides the field effect at extrinsic doping conditions, in terms of
multiple dopant diffusion, the diffusivities of the dopants themselves
have to be taken into account being concentration depended. Because
point defects exist in either neutral (0), single (+,-) or
double charged (+ +,- -) states [Fai81], the effective
diffusion coefficient becomes
DA = DAX0 + DAX+ .  
 + DAX- .
+ DAX- . 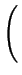 
 + DAX- - .
+ DAX- - .  
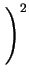 |
|
|
(2.19) |
where X denotes a point defect (interstitial or vacancy) and
CXi the concentrations under intrinsic conditions.
Again the temperature dependence of each diffusivity component can be
modeled by an Arrhenius law.
DAX = D0 . e-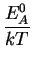 |
|
|
(2.20) |
The diffusivities for the most common dopants under extrinsic
conditions are shown in Table 2.2 after [TMA97].
Table 2.2:
Arrhenius parameters for the diffusivities of boron, arsenic, phosphorus and antimony
| Dopant |
D0 |
EA0 |
Di+ |
EA+ |
Di- |
EA- |
Di- - |
EA- - |
| |
[cm2/s] |
[eV] |
[cm2/s] |
[eV] |
[cm2/s] |
[eV] |
[cm2/s] |
[eV] |
| B |
4.10 |
3.46 |
2.16 |
3.46 |
- |
- |
- |
- |
| As |
0.37 |
3.44 |
- |
- |
5.47 |
3.44 |
- |
- |
| P |
23.10 |
3.66 |
- |
- |
26.64 |
4.00 |
26.52 |
4.37 |
| Sb |
0.42 |
3.65 |
- |
- |
4.5 |
4.08 |
- |
- |
|


Next: 2.1.3 Segregation
Up: 2.1 Diffusion
Previous: 2.1.1 Extrinsic Dopant Diffusion
Mustafa Radi
1998-12-11
