



Next: A.1.2.2 Subthreshold Current
Up: A.1.2 The Concrete MOSFET
Previous: A.1.2 The Concrete MOSFET
When
 the electron density in the channel in thermal equilibrium
is larger than the hole density in the bulk,
the electron density in the channel in thermal equilibrium
is larger than the hole density in the bulk,
 ,
which is called
the strong-inversion condition.
In this case the drain current in the linear region and saturation region
can be approximately described using the same equations
as for the structure in Fig. A.1:
,
which is called
the strong-inversion condition.
In this case the drain current in the linear region and saturation region
can be approximately described using the same equations
as for the structure in Fig. A.1:
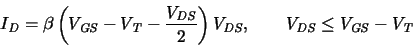 |
(A.11) |
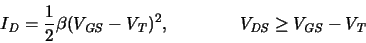 |
(A.12) |
where the conductance parameter
 is defined as
is defined as
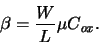 |
(A.13) |
Note, that these equations are valid only for devices with
electrically long channels, i.e.,
 .
Furthermore, as the depletion zone, which determines
.
Furthermore, as the depletion zone, which determines
 ,
actually depends on the electrostatic potential in the
channel and on the source and drain voltages, these
equations can be quite inaccurate for realistic devices with
smaller dimensions and more aggressive operating conditions.
,
actually depends on the electrostatic potential in the
channel and on the source and drain voltages, these
equations can be quite inaccurate for realistic devices with
smaller dimensions and more aggressive operating conditions.
G. Schrom
![]() the electron density in the channel in thermal equilibrium
is larger than the hole density in the bulk,
the electron density in the channel in thermal equilibrium
is larger than the hole density in the bulk,
![]() ,
which is called
the strong-inversion condition.
In this case the drain current in the linear region and saturation region
can be approximately described using the same equations
as for the structure in Fig. A.1:
,
which is called
the strong-inversion condition.
In this case the drain current in the linear region and saturation region
can be approximately described using the same equations
as for the structure in Fig. A.1: