Equation (4.24) represents a Fredholm integral equation of second kind with a free term determined by function
 . This equation can
be rewritten4.4:
. This equation can
be rewritten4.4:
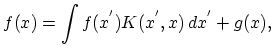 |
(4.25) |
where the
 and the free term are given functions. The multidimensional variable
and the free term are given functions. The multidimensional variable  stands for
stands for
 4.5. The resolvent series4.6 of a Fredholm integral equation is obtained by replacement of its right hand side into itself:
4.5. The resolvent series4.6 of a Fredholm integral equation is obtained by replacement of its right hand side into itself:
 |
(4.26) |
This means that the solution of (4.24) can be written as consecutive iterations of the free term:
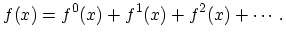 |
(4.27) |
To find the iteration terms explicitly (4.24) is rewritten as:
where
 has been replaced by
has been replaced by
 and the respective quasi-momentum space trajectory is:
and the respective quasi-momentum space trajectory is:
Introducing a quasi-momentum space trajectory for the time interval
 :
:
| |
|
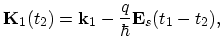 |
|
| |
|
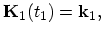 |
(4.30) |
one obtains for
 :
:
Substituting (4.32) into (4.29) gives:
From (4.34) the first iteration term is obtained:
| |
|
 |
|
| |
|
![$\displaystyle \int_{0}^{t}\,dt_{1}\int\,d\vec{k}_{1}G(\vec{K}_{1}(0))\exp\biggl...
...(t_{1}))\exp\biggl(-\int_{t_{1}}^{t}\widetilde{\lambda}[\vec{K}(y)]\,dy\biggr).$](img913.png) |
(4.33) |
which is also schematically shown in Fig. 4.1.
Figure 4.1:
Graphical representation of the first iteration term.
|
|
In order to obtain the second iteration term the third quasi-momentum space trajectory is introduced for

| |
|
 |
|
| |
|
 |
(4.34) |
Then for
 in (4.32) one obtained:
in (4.32) one obtained:
The second iteration term is obtained from (4.36) by replacing
 with the free term of (4.29):
with the free term of (4.29):
| |
|
![$\displaystyle f_{1}^{(2)}(\vec{k},t)=\int_{0}^{t}\,dt_{1}\int\,d\vec{k}_{1}\int...
...exp\biggl(-\int_{0}^{t_{2}}\widetilde{\lambda}[\vec{K}_{2}(y)]\,dy\biggr)\times$](img923.png) |
|
| |
|
![$\displaystyle \times\widetilde{S}(\vec{k}_{2},\vec{K}_{1}(t_{2}))\exp\biggl(-\i...
...(t_{1}))\exp\biggl(-\int_{t_{1}}^{t}\widetilde{\lambda}[\vec{K}(y)]\,dy\biggr).$](img924.png) |
(4.36) |
This term is displayed graphically in Fig. 4.2.
Figure 4.2:
Graphical representation of the second iteration term.
|
|
S. Smirnov:
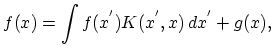

![$\displaystyle \int_{0}^{t}\,dt_{1}\int\,d\vec{k}_{1}G(\vec{K}_{1}(0))\exp\biggl...
...(t_{1}))\exp\biggl(-\int_{t_{1}}^{t}\widetilde{\lambda}[\vec{K}(y)]\,dy\biggr).$](img913.png)
![]()