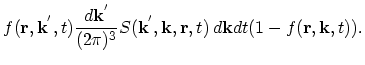It is convenient to define a quantity
 to express the electron number per unit volume with quasi-momenta
in the infinitesimal volume
to express the electron number per unit volume with quasi-momenta
in the infinitesimal volume  around
around  and which have been scattered during the infinitesimal time interval
and which have been scattered during the infinitesimal time interval  :
:
 |
(2.50) |
As the volume  is infinitesimal, the scattering results in an electron being removed from this volume. Therefore
(2.50) can also be considered as the number of electrons which are lost from the volume
is infinitesimal, the scattering results in an electron being removed from this volume. Therefore
(2.50) can also be considered as the number of electrons which are lost from the volume  around
around  during the time interval
during the time interval  due to scattering.
due to scattering.
The quantity
 can be found from the fact that the expression
can be found from the fact that the expression
is the probability that any electron from the vicinity of point  has been scattered during the time interval
has been scattered during the time interval  and thus the total number of
the scattered electrons in
and thus the total number of
the scattered electrons in  around
around  is equal to
is equal to
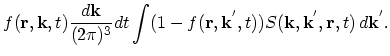 |
(2.51) |
Comparison with (2.50) gives
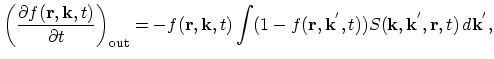 |
(2.52) |
where the minus sign shows that this quantity describes the loss of electrons.
Scattering processes can change the distribution function in the opposite way. In addition to the scattering out
of the domain  there also exist scattering processes leading to a gain of electrons in
there also exist scattering processes leading to a gain of electrons in  . To describe these processes it is
natural to introduce the quantity
. To describe these processes it is
natural to introduce the quantity
 defined so that the expression
defined so that the expression
 |
(2.53) |
gives the number of electrons per unit volume which are scattered into the volume  around
around  during the infinitesimal time interval
during the infinitesimal time interval  .
In order to find
.
In order to find
 it is necessary to consider electrons in
it is necessary to consider electrons in
 near
near
 which
are scattered into
which
are scattered into  and sum over all possible
and sum over all possible
 . The total number of electrons in
. The total number of electrons in
 is equal to
is equal to
 . From this number of electrons only
. From this number of electrons only
 would be
scattered into
would be
scattered into  around
around  during
during  if the corresponding states were not occupied. However only the fraction
if the corresponding states were not occupied. However only the fraction
 of the states are available. Thus, the total number of electrons per unit volume scattered into
of the states are available. Thus, the total number of electrons per unit volume scattered into  around
around  from
from
 around
around
 during
during  is equal to
is equal to
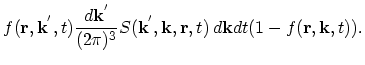 |
(2.54) |
Summing over all possible
 and comparing with (2.53) gives:
and comparing with (2.53) gives:
 |
(2.55) |
Now the collision integral in (2.46) can be expressed as a sum of two terms:
It should be noted that in the non-degenerate case when
 the scattering operator can be rewritten as:
the scattering operator can be rewritten as:
 |
(2.57) |
where the total scattering rate
 is defined as follows:
is defined as follows:
 |
(2.58) |
The Boltzmann equation takes now the form:
S. Smirnov:
![]() can be found from the fact that the expression
can be found from the fact that the expression

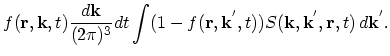
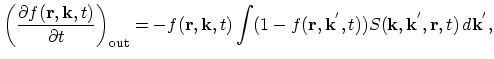
![]() there also exist scattering processes leading to a gain of electrons in
there also exist scattering processes leading to a gain of electrons in ![]() . To describe these processes it is
natural to introduce the quantity
. To describe these processes it is
natural to introduce the quantity
![]() defined so that the expression
defined so that the expression