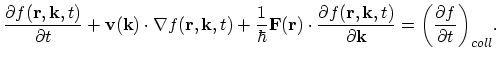2.3.2 Collision Integral

If the scattering events could be neglected, each electron would represent a closed subsystem and equation (2.44) would completely determine the distribution function of an electron. The time derivative means here the differentiation along the semiclassical trajectory in the phase space of an individual electron. If an external force field acts on the electron system, the total time derivative can be expressed as:

$$\frac{df}{dt}=\frac{\partial f(\vec{r},\vec{k},t)}{\partial t}+\v... ...ar}\vec{F}(\vec{r})\cdot\frac{\partial f(\vec{r},\vec{k},t)}{\partial \vec{k}},$$ (2.45)

where $\vec{F}(\vec{r})$ is the total external force given by (2.15).

If collisions are taken into consideration, Liouville's theorem is violated and the distribution function is no longer constant along semiclassical phase space trajectories. Instead of (2.44) one should write:

$$\frac{df}{dt}=\biggl(\frac{\partial f}{\partial t}\biggr)_\mathrm{coll},$$ (2.46)

where the right hand side is called the collision integral or scattering operator^2.17. The collision integral is thus defined as the rate of change of the distribution function, that is, $\bigl(\frac{\partial f}{\partial t}\bigr)_\mathrm{coll}\frac{d\vec{r}d\vec{k}}{(2\pi)^{3}}$ is the change of the electron number per unit time in the phase space volume $d\vec{r}d\vec{k}$ due to scattering. Combining (2.45) and (2.46) gives the following equation:

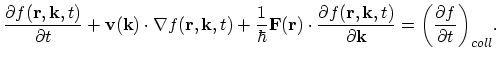$$\frac{\partial f(\vec{r},\vec{k},t)}{\partial t}+\vec{v}(\vec{k})... ...ec{k},t)}{\partial \vec{k}}=\biggl(\frac{\partial f}{\partial t}\biggr)_{coll}.$$ (2.47)

Equations of this type represent kinetic equations in a general form. In the case of gases including the electron gas in solids it is usually called the Boltzmann kinetic equation. The kinetic equation takes a real meaning only when the form of the collisional integral is found. This form can be found accounting for electrons which are scattered in and out of a given phase space domain. The number of these electrons can be obtained introducing the scattering rate. In general each scattering mechanism is described by a scattering rate which can be found using the quantum mechanical scattering theory for an electron and the scattering center.
S. Smirnov: