2.4.1.3 Band Structure Periodicity

For two wave vectors $\vec{k}$ and $\vec{k}+\vec{K}$ the solutions of Schrödinger equation (2.68) are related to each other as $\exp(i\vec{K}\cdot\vec{r})u_{n\vec{k}+\vec{K}}(\vec{r})=u_{n\vec{k}}(\vec{r})$. This leads to equal eigenvalues

$$\epsilon_{n}(\vec{k})=\epsilon_{n}(\vec{k}+\vec{K}),$$ (2.70)

and equal wave functions

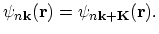$$\psi_{n\vec{k}}(\vec{r})=\psi_{n\vec{k}+\vec{K}}(\vec{r}).$$ (2.71)

It can be seen that each energy branch has the same period as the reciprocal lattice. As the functions $\epsilon_{n}(\vec{k})$ are periodic, they have maxima and minima which determine the width of the bands.

It should be noted that the wave vector $\vec{k}$ in (2.66) can always be chosen in a way to belong to the first Brillouin zone because any vector $\vec{k}^{'}$ out of the first Brillouin zone can be represented as the sum $\vec{k}^{'}=\vec{k}+\vec{K}$, where $\vec{K}$ is a vector of the reciprocal lattice. Using the equivalent form of Bloch's theorem:

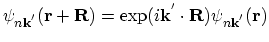$$\psi_{n\vec{k}^{'}}(\vec{r}+\vec{R})=\exp(i\vec{k}^{'}\cdot\vec{R})\psi_{n\vec{k}^{'}}(\vec{r})$$ (2.72)

together with (2.71) and the equality $\exp(i\vec{K}\cdot\vec{R})=1$ one obtains (2.72) for vector $\vec{k}$. S. Smirnov: