2.5.1.1 First Order Perturbation

Let

denote a set of quantum numbers which characterize states of an unperturbed system. The corresponding wave functions are $\psi_{s}$ and satisfy the unperturbed Schrödinger equation

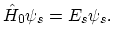$\displaystyle \hat{H}_{0}\psi_{s}=E_{s}\psi_{s}.$

(2.86)

In the case of one electron in the lattice,

represents a band index

and the components of the quasi-momentum $\vec{p}=\hbar\vec{k}$ , and $\psi_{s}$ is Bloch's wave function given by (2.66). For electrons in a vibrating lattice

includes in addition phonon numbers in all possible states and $\psi_{s}$ is the product of a Bloch wave and the crystal wave function. Bloch's wave functions and the normal lattice modes are subject to the usual periodic boundary conditions in a cube. The wave functions $\psi_{s}$ are ortho-normalized. Due to the interaction Hamiltonian $\hat{H}_\mathrm{int}$ the wave function $\psi_{s}$ turns into a new wave function $\Psi$ . At the initial time

the system is unperturbed which means $\Psi(t=0)=\psi_{s}$ . At

$\Psi$ is determined by the equation^2.28

$\displaystyle i\hbar\frac{\partial\Psi}{\partial t}=\hat{H}\Psi.$

(2.87)

In the absence of the interaction equation (2.87) has the usual solution: $\Psi=\psi_{s}\exp(-iE_{s}t/\hbar)$ . When the interaction is present $\Psi(t)$ can be represented as a series

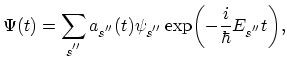$$\displaystyle \Psi(t)=\sum_{s^{$

(2.88)

where $$ a_{s^{$ are yet unknown coefficients. Quantities $$ \vert a_{s^{$ are the probabilities of finding the system in state $$ s^{$ at time

. They satisfy the condition

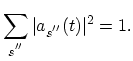$$\displaystyle \sum_{s^{$

(2.89)

Substituting (2.88) into (2.87) and forming the inner product $\langle a_{s^{'}}\vert\Psi\rangle$ gives the equation for coefficients $$ a_{s^{$ :

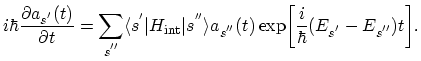$$\displaystyle i\hbar\frac{\partial a_{s^{'}}(t)}{\partial t}=\sum_{s^{$

(2.90)

In the first order perturbation the unperturbed values of $$ a_{s^{$ are used in the right hand side^2.29 of (2.90). The unperturbed values of $$ a_{s^{$ follows from (2.88)^2.30:

$\displaystyle i\hbar\frac{\partial a_{s^{'}}}{\partial t}=\langle s^{'}\vert H_\mathrm{int}\vert s\rangle\exp\biggl[\frac{i}{\hbar}(E_{s^{'}}-E_{s})t\biggr].$

(2.91)

The solution of this equation is

$\displaystyle a_{s^{'}}(t)=\frac{-1+\exp\biggl[\frac{i}{\hbar}(E_{s^{'}}-E_{s})t\biggr]}{E_{s}-E_{s^{'}}}\langle s^{'}\vert H_\mathrm{int}\vert s\rangle.$

(2.92)

Therefore the probability of finding a system at time

in state $s^{'}$ is

$\displaystyle \vert a_{s^{'}}(t)\vert^{2}=\frac{2\biggl[1-\cos\biggl(\frac{E_{s... ...-E_{s^{'}})^{2}} \vert\langle s^{'}\vert H_\mathrm{int}\vert s\rangle\vert^{2}.$

(2.93)

The transition probability per unit time is equal to the time derivative of (2.93):

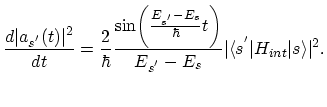$\displaystyle \frac{d\vert a_{s^{'}}(t)\vert^{2}}{dt}=\frac{2}{\hbar} \frac{\si... ...biggr)}{E_{s^{'}}-E_{s}}\vert\langle s^{'}\vert H_{int}\vert s\rangle\vert^{2}.$

(2.94)

S. Smirnov:


Previous: 2.5.1 Perturbation Theory Up: 2.5.1 Perturbation Theory Next: 2.5.1.2 Fermi's Golden Rule