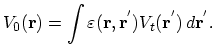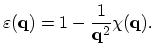The screening effect is the most important manifestation of the electron-electron interaction. In this work only linear screening is
considered. Nonlinear effects which require the solution of the nonlinear Poisson equation either analytically [46,47] or
numerically [48] are neglected here.
A positively charged particle introduced into the electron gas will create an excess of negative charge in its vicinity which screen its
electric field2.35. The bare potential (2.142) satisfies the Poisson equation:
 |
(2.144) |
where
![$ \rho_{0}(\vec{r})=Ze[\delta(\vec{r})+\delta(\vec{r}-\vec{R})]$](img593.png) is the volume density of the particle charge2.36. The total physical potential
is the volume density of the particle charge2.36. The total physical potential
 , which is produced both by the particle and the electron cloud, is described by the Poisson
equation of the form:
, which is produced both by the particle and the electron cloud, is described by the Poisson
equation of the form:
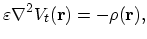 |
(2.145) |
where
 is the total volume charge density:
is the total volume charge density:
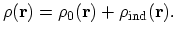 |
(2.146) |
Here
 denotes the volume density of the charge induced in the electron gas by the positive particle. From the electrodynamics
of continuous media [49] it is known that
denotes the volume density of the charge induced in the electron gas by the positive particle. From the electrodynamics
of continuous media [49] it is known that
 and
and
 are linearly related to each other:
are linearly related to each other:
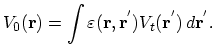 |
(2.147) |
For the homogeneous electron gas function
 can only depend on the distance between the two points
can only depend on the distance between the two points  and
and
 :
:
 |
(2.148) |
This gives the following relation between the Fourier components of
 and
and
 :
:
 |
(2.149) |
In the linear screening theory it is assumed that
 and
and
 are linearly related to each other2.37 which implies for Fourier components:
are linearly related to each other2.37 which implies for Fourier components:
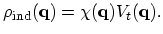 |
(2.150) |
The Fourier transform of the Poisson equations (2.144) and (2.145) together with (2.150) leads to the relation:
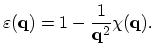 |
(2.151) |
To calculate the quantity
 some approximations are necessary. In this work we use the so called Lindhard screening
theory2.38. Within this model the expression for the dielectric function [50]
is:
some approximations are necessary. In this work we use the so called Lindhard screening
theory2.38. Within this model the expression for the dielectric function [50]
is:
 |
(2.152) |
with the inverse screening length given by the Thomas-Fermi theory:
 |
(2.153) |
Here
 stands for the Fermi integral of the
stands for the Fermi integral of the  -th order, and
-th order, and  is the reduced Fermi energy:
is the reduced Fermi energy:
 |
(2.154) |
 represents the screening function given by the following expression:
represents the screening function given by the following expression:
 |
(2.155) |
where the argument  is:
is:
 |
(2.156) |
The corrections described above can be taken into account within the first Born approximation. In this approximation the scattering amplitude is given as:
 |
(2.157) |
where
 is defined by
is defined by
 |
(2.158) |
The differential cross section is defined as:
 |
(2.159) |
Now the total scattering rate is obtained through
 |
(2.160) |
where
 is the density of scattering pairs and
is the density of scattering pairs and
 is equal to:
is equal to:
 |
(2.161) |
The simple calculations give the final total ionized impurity scattering rate taking into account the momentum dependent screening and the two-ion
correction:
| |
|
 |
|
| |
|
 |
(2.162) |
S. Smirnov: