3.1.1 Critical Thickness and Dislocations

The basic principle of strained-layer epitaxy is that a certain amount of elastic strain can be accommodated by any material without generating dislocations or defects. It takes energy to accommodate an epitaxial layer of lattice-mismatched material. The energy depends on both the thickness and the size of the lattice mismatch. It also requires energy to create a dislocation that will relieve the lattice mismatch strain. If the thickness of the epitaxial layer is kept small enough to maintain the elastic strain energy below the energy of dislocation formation, the strained-layer structure will be thermodynamically stable against dislocation formation. The unstrained state of the lattice-mismatched layer is energetically most favorable, but the strained structure is stable against transformation to the unstrained state by the energy barrier associated with the generation of enough dislocations to relieve the strain.

The most important types are edge and screw dislocations. Edge dislocation can be represented by an extra half plane inserted into a crystal as illustrated in Fig. 3.1. The edge of this half plane is called an edge dislocation. In the vicinity of the dislocation the deviation of

Figure 3.1: Edge dislocation.

the crystal structure from the ideal one is rather strong. But already at distances of a few lattice periods the crystal planes touch each other almost as in the perfect crystal structure. However, the deformation also exists at great distance from the dislocation. It can be clearly found by traversing a closed contour through the lattice nodes in $x-y$ plane containing the origin of the coordinates. If $\vec{u}$ stands for the displacement of an atom from its position in the ideal structure, the total change of this vector for the whole contour is not equal to zero. Instead it is equal to the lattice period along $x$.

Screw dislocations can be viewed as a result of cutting a lattice along a half plane with a subsequent one period relative shift of the two parts of the lattice on each side of the cut as depicted in Fig. 3.2. The edge of the cut is called the screw dislocation. Traversing a contour around the

Figure 3.2: Screw dislocation.

dislocation line the vector $\vec{u}$ gains one period along this axis. From the macroscopic point of view a dislocation deformation of a crystal considered as a continuous media has a general property: traversing a closed contour $L$ containing the dislocation line $D$, the vector of the elastic shift $\vec{u}$ gains a finite addition $\vec{b}$ equal to one of the periods of a given crystal lattice. The constant vector $\vec{b}$ is called Burger's vector of a given dislocation. This property is mathematically written as:

$$\oint_{L}\,du_{i}=\oint_{L}\frac{\partial u_{i}}{\partial x_{k}}\,dx_{k}=-b_{i},$$ (3.1)

where it is understood that the traversing direction of the contour is clockwise with respect to the chosen direction of the tangent vector $\vec{\tau}$ of the dislocation line. The dislocation line itself represents a line of peculiar points of the deformation field. In the case of edge and screw dislocations the dislocation lines $D$ represent straight lines with $\vec{\tau}\perp\vec{b}$ and $\vec{\tau}\parallel\vec{b}$, respectively. In the general case a dislocation is a curve along which the angle between $\vec{\tau}$ and $\vec{b}$ can change. A dislocation line cannot stop inside a crystal. The two ends must be on the surface of a crystal or the dislocation represents a loop. Condition (3.1) means that the displacement vector is a non-unique function of coordinates. It gains an additional vector after traversing a contour around a dislocation line. Physically there does not exist any non-uniqueness: an additional vector $\vec{b}$ means an additional one period shift of the lattice nodes which cannot change the lattice state. In particular, the stress tensor is a unique and continuous function of coordinates.

A fundamental assumption underlying many of the critical thickness calculations is the a priori assumption that the equilibrium configuration of the strain induced dislocations is that of a regular, non-interacting, rectangular array. Critical layer thicknesses are then computed by requiring that the total strain energy per unit area $\epsilon_{T}$ be a minimum with respect to the in-plane strain $e$

$$\frac{\partial\epsilon_{T}}{\partial\arrowvert e\arrowvert}=0$$ (3.2)

evaluated at $\arrowvert e\arrowvert=f$, where $f$ is the mismatch between the film and the substrate. Here $\epsilon_{T}$ is defined as a sum

$$\epsilon_{T}=\epsilon_{H}+\epsilon_{D}$$ (3.3)

of the homogeneous strain energy density $\epsilon_{H}$:

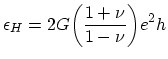$$\epsilon_{H}=2G\biggl(\frac{1+\nu}{1-\nu}\biggr)e^{2}h$$ (3.4)

and the areal energy density of the dislocation $\epsilon_{D}$:

$$\epsilon_{D}\equiv\frac{E_{l}}{p}.$$ (3.5)

Here $G$ is the shear modulus, $h$ is the film thickness, $E_{l}$ the energy per unit length of a given dislocation line, and $p$ is the spacing between the dislocations in the assumed rectangular array. It should be noted that $E_{l}$ is independent of the in-plane strain $e$ in the film [53] and in fact $\epsilon_{D}$ only depends on the strain in the film through of the strain-dependence of the effective interfacial width $p$. The spacing between dislocations in the array is given by

$$p=\frac{b}{f-\arrowvert e\arrowvert}$$ (3.6)

where $b$ is the magnitude of Burger's vector. Equations (3.4)-(3.6) in conjuction with the mechanical equilibrium condition (3.2) give the following equation [54] for the critical thickness $h_{c}$:

$$h_{c}=\frac{b}{4\pi f(1+\nu)}\biggl[\ln\biggl(\frac{h_{c}}{b}\biggr)+1\biggr].$$ (3.7)

However there are other models for the critical thickness $h_{c}$. One of them can be described by the expression [55]:

$$h_{c}=\frac{b^{2}(1-\nu)}{20\pi\sqrt{2}f^{2}\langle a(x)\rangle(1+\nu)}\ln\biggl(\frac{h_{c}}{b}\biggr).$$ (3.8)

The difference between the models (3.7) and (3.8) lies in the fact that in deriving (3.8) it is not assumed that initial dislocations appear in a regular rectangular array. Here dislocations are generated in a stochastic fashion. This is an attempt to deal with the relaxation kinetics in contrast to the equilibrium based derivation (3.7). It is assumed that dislocation formation requires in a dislocation formation energy $\epsilon_{D}$. As the thickness of a film approaches its critical value, some fraction of the homogeneous strain energy $\epsilon_{H}$ will be used to supply this dislocation formation energy.

S. Smirnov: