



Next: Bibliography
Up: Dissertation Oliver Triebl
Previous: 8. Conclusions and Outlook
A. Derivation of the Impact-Ionization Integral
In the following the derivation of the impact-ionization integral from
Section 5.1.2 will be given. First, the differntial equation
 |
(A.1) |
has to be solved. Using the simplified notation
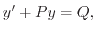 |
(A.2) |
with
 and
and
 one can derive the
homogenous solution
one can derive the
homogenous solution
 |
(A.3) |
where C is the constant of integration. Applying the method of variation of
constants, the ansatz of the particular solution  is derived from the
homogenous solution, using
is derived from the
homogenous solution, using
 This ansatz function
This ansatz function  can
be differentiated to
can
be differentiated to
 |
(A.4) |
Comparison of the coefficients between equations (A.2) and (A.4) gives
 |
(A.5) |
and  evaluates to
evaluates to
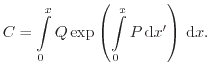 |
(A.6) |
This leads to the particular solution
![$\displaystyle y_p = \exp \left( - \int_0^x P \ensuremath{ \mathrm{d}}x \right)...
...t_0^x P \ensuremath{ \mathrm{d}}x' \right) \ensuremath{ \mathrm{d}}x \right ]$](img784.png) |
(A.7) |
and together with the homogenous solution  to the solution
of (A.2)
to the solution
of (A.2)
![$\displaystyle y = \exp \left( - \int_0^x P \ensuremath{ \mathrm{d}}x \right) \...
...P \ensuremath{ \mathrm{d}}x' \right) \ensuremath{ \mathrm{d}}x + C \right ] .$](img786.png) |
(A.8) |
Using (A.8) our initial problem
(A.1) solves together with the boundary conditions
 and
and
 to
to
![$\displaystyle I_p = I \exp \left( \int_0^x \left( \ensuremath{\alpha _p}- \ensu...
...h{ \mathrm{d}}x' \right) \ensuremath{ \mathrm{d}}x + \frac{1}{M_p} \right ] .$](img789.png) |
(A.9) |
To simplify the solution (A.9) the following
relationship can be used. Considering
 |
(A.10) |
the following simplification can be performed:
 |
(A.11) |
Making the relation (A.11) applicable, (A.9)
can be rewritten at the position  as
as
![$\displaystyle 1 = \exp \left( \int_0^W \left( \ensuremath{\alpha _p}- \ensurema...
...,\mathrm{d}}x' \right) + 1} + \frac{1}{M_p} \left. \vphantom{\int_0^W} \right ]$](img793.png) |
(A.12) |
and simplified to
 |
(A.13) |




Next: Bibliography
Up: Dissertation Oliver Triebl
Previous: 8. Conclusions and Outlook
O. Triebl: Reliability Issues in High-Voltage Semiconductor Devices



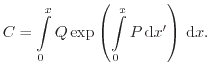
![$\displaystyle y_p = \exp \left( - \int_0^x P \ensuremath{ \mathrm{d}}x \right)...
...t_0^x P \ensuremath{ \mathrm{d}}x' \right) \ensuremath{ \mathrm{d}}x \right ]$](img784.png)

![$\displaystyle 1 = \exp \left( \int_0^W \left( \ensuremath{\alpha _p}- \ensurema...
...,\mathrm{d}}x' \right) + 1} + \frac{1}{M_p} \left. \vphantom{\int_0^W} \right ]$](img793.png)
