3.7.1 Effective Electron Mass in Unstrained Si

The conduction band minima of Si lie on the $\langle 001\rangle$ axes at points ${\ensuremath{\mathitbf{k}}}_\mathrm{min}$ distant $0.15 \frac{2\pi}{a_0}$ from the $X$ symmetry points. From the knowledge of the eigenenergies $E_{n{\ensuremath{\mathitbf{k}}}_0}$ and the wavefunctions $u_{n{\ensuremath{\mathitbf{k}}}_0}$ at the conduction band minima ${\ensuremath{\mathitbf{k}}}_0$, the eigenvalues $E_{n{\ensuremath{\mathitbf{k}}}}$ at neighboring points $\mathitbf{k}$ can be expanded to second order in $k_i$ in terms of the unperturbed wavefunctions and eigenenergies using nondegenerate perturbation theory

$$E_{n{\ensuremath{\mathitbf{k}}}} = E_{n{\ensuremath{\mathitbf{k}}... ...}{E_{n{\ensuremath{\mathitbf{k}}}_0}-E_{n'{\ensuremath{\mathitbf{k}}}_0}}k_j\ .$$ (3.62)

Here, we used the index notation $\sum_{i=1}^3 k_i p_i$ for ${\ensuremath{\mathitbf{k}}} \cdot {\ensuremath{\mathitbf{p}}}$ and Dirac's notation for the matrix elements

$$\langle u_{n{\ensuremath{\mathitbf{k}}}_0}\vert p_j \vert u_{n'{\... ...{\hbar}{i} \frac{\partial}{\partial x_j} u_{n'{\ensuremath{\mathitbf{k}}}_0}\ .$$ (3.63)

Linear terms in $k_i$ vanish because $E_{n{\ensuremath{\mathitbf{k}}}_0}$ has been assumed to be a minimum. The dispersion relation (3.62) can be rewritten in terms of the effective mass tensor $m^\ast_{n,ij}$ of band $n$

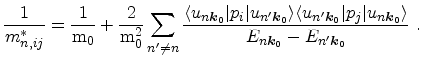$$\frac{1}{m^\ast_{n,ij}} = \frac{1}{\ensuremath{\mathrm{m}}_0} + \... ...le }{E_{n{\ensuremath{\mathitbf{k}}}_0}-E_{n'{\ensuremath{\mathitbf{k}}}_0}}\ .$$ (3.64)

In crystals with diamond structure, the effective mass tensor for the lowest conduction band $\Delta _1$ is diagonal and can be characterized by two masses. For the [001] valley one obtains in the principal coordinate system

$$\frac{1}{\ensuremath{m_\mathrm{l}}} = \frac{1}{\ensuremath{\mathrm{m}}_0} + \frac{2}{\ensuremath{\mat... ...\Delta_1 {\ensuremath{\mathitbf{k}}}_0}-E_{n'{\ensuremath{\mathitbf{k}}}_0}}\ ,$$ (3.65)

$$\frac{1}{\ensuremath{m_\mathrm{t}}} = \frac{1}{\ensuremath{\mathrm{m}}_0} + \frac{2}{\ensuremath{\mat... ...\Delta_1 {\ensuremath{\mathitbf{k}}}_0}-E_{n'{\ensuremath{\mathitbf{k}}}_0}}\ ,$$ (3.66)

where $\Delta _1$ denotes the band index $n$ of the lowest conduction band. Thus, the energy dispersion (3.62) can be written in the form of (3.28).

The derived equations show that because of the coupling between electronic states in different bands via the ${\ensuremath{\mathitbf{k}}}\!\cdot\!{\ensuremath{\mathitbf{p}}}$ term, an electron in a solid has a mass different from that of a free electron. The coupling terms depend on two factors

1. The separation in energy between two bands $n$ and $n'$ determines the relative importance of the contribution of band $n'$ to the effective mass of band $n$. The bigger the energetic gap between two bands the smaller is the effect on the effective mass.
2. The matrix element theorem [Tinkham64] can be used to find all bands $n'$ that have nonzero matrix elements $\langle u_{n{\ensuremath{\mathitbf{k}}}_0}\vert{\ensuremath{\mathitbf{k\cdot p}}}\vert u_{n'{\ensuremath{\mathitbf{k}}}_0}\rangle$ by applying group theoretical considerations to determine all possible symmetries $u_{n'{\ensuremath{\mathitbf{k}}}_0}$ can have.

Using the empirical pseudopotential method for band structure calculations (see Section 3.8) it is possible to numerically evaluate the matrix elements and hence to obtain the effective masses from (3.64).

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology