3.7 The kp method

Using the kp method [Bir74,Yu03] one can obtain analytical expressions for the band dispersion and the effective masses. It allows the extrapolation of the band structure over the entire Brillouin zone from the energy gaps and optical matrix elements at the zone center. While the kp theory has been frequently used to model the valence band of semiconductors, we will additionally apply it to model the impact of strain on the conduction band minimum.

The kp method can be derived from the one-electron Schrödinger equation

$$\mathcal{H} \phi_n({\ensuremath{\mathitbf{r}}}) = \left (\frac{p^... ...phi_n({\ensuremath{\mathitbf{r}}}) = E_n \phi_n({\ensuremath{\mathitbf{r}}})\ .$$ (3.58)

Here $\mathcal{H}$ denotes the one-electron Hamilton operator and $V({\ensuremath{\mathitbf{r}}})$ the periodic lattice potential. The wavefunction of an electron in an eigenstate labeled $n$ and its energy are denoted by $\phi_n({\ensuremath{\mathitbf{r}}})$ and $E_n$, respectively. In a periodic potential Bloch's theorem applies, and the solutions of (3.58) can be expressed as

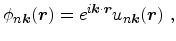$$\phi_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}}) ... ...\mathitbf{r}}}}u_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})\ ,$$ (3.59)

where $n$ is the band index, ${\ensuremath{\mathitbf{k}}}$ a wave vector, and $u_{n{\ensuremath{\mathitbf{k}}}}(r)$ has the periodicity of the lattice. Assuming that the potential $V({\ensuremath{\mathitbf{r}}})$ is local^3.1, one can substitute $\phi_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})$ into (3.58) to obtain an equation for $u_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})$

$$\left ( \frac{p^2}{2m} + V({\ensuremath{\mathitbf{r}}}) + \frac{\... ...^2}{2m}\right )u_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})\ .$$ (3.60)

Considering any fixed wavevector ${\ensuremath{\mathitbf{k}}} = {\ensuremath{\mathitbf{k}}}_0$, the above equation yields a complete set of eigenfunctions $u_{n{\ensuremath{\mathitbf{k}}}_0}$, which completely span the space of lattice periodic functions in the real space. Hence, the wavefunction $\phi_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})$ at ${\ensuremath{\mathitbf{k}}}$ can be expanded in terms of $u_{n{\ensuremath{\mathitbf{k}}}_0}$

$$\phi_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}}) ... ...thitbf{k}}} {\ensuremath{\mathitbf{r}}}} u_{n'{\ensuremath{\mathitbf{k}}}_0}\ .$$ (3.61)

Once, $E_{n{\ensuremath{\mathitbf{k}}}_0}$ and $u_{n{\ensuremath{\mathitbf{k}}}_0}$ are known, the functions $\phi_{n{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})$ and the eigenenergies $E_{n{\ensuremath{\mathitbf{k}}}}$ at any $\mathitbf{k}$ vector ${\ensuremath{\mathitbf{k}}}_0 + \Delta {\ensuremath{\mathitbf{k}}}$ in the vicinity of ${\ensuremath{\mathitbf{k}}}_0$ can be obtained by treating the term $\hbar \Delta {\ensuremath{\mathitbf{k}}} \cdot {\ensuremath{\mathitbf{p}}}/m$ in (3.60) as a perturbation. Either degenerate or nondegenerate perturbation theory has to be used. The method has been first applied by Seitz [Seitz35] and was later extended to study the band structure of semiconductors [Luttinger55,Kane56,Cardona66].

This method for calculating the band structure is known as the kp method. It works best for small $\Delta {\ensuremath{\mathitbf{k}}}$ and can be applied to calculate the band structure near any given point ${\ensuremath{\mathitbf{k}}}_0$ provided that the matrix elements of ${\ensuremath{\mathitbf{p}}}$ between the wavefunctions (or the wavefunctions themselves) and the energies at ${\ensuremath{\mathitbf{k}}}_0$ are known. When using a sufficiently large number of $u_{n{\ensuremath{\mathitbf{k}}}_0}$ to approximate a complete set of basis functions, the band structure over the entire first Brillouin zone can be calculated by diagonalizing (3.60) numerically [Cardona66].

In the following, a nondegenerate kp theory will be used to derive the band dispersion and the effective masses for the nondegenerate conduction band of Si. To analyze the effect of shear strain on the lowest conduction band $\Delta _1$, a degenerate kp method is adopted in Section 3.7.2, since the $\Delta _1$ conduction band is expanded around the symmetry point $X$ (zone boundary) where it touches the $\Delta _{2'}$ conduction band.

Subsections

• 3.7.1 Effective Electron Mass in Unstrained Si
• 3.7.2 Strain Effect on the Si Conduction Band Minimum
  • Energy Dispersion of the Conduction Band Minimum of Strained Si: Method 1
  • Energy Dispersion of the Conduction Band Minimum of Strained Si: Method 2
  • Discussion

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology