3.8.1 The Empirical Pseudopotential Method

The pseudopotential theory is based on an ansatz which separates the total wave function into an oscillatory part and a smooth part, the so called pseudo wave function. The strong true potential of the ions is replaced by a weaker potential valid for the valence electrons, the pseudopotential $V({\ensuremath{\mathitbf{r}}})$, which approaches the unscreened Coulomb potential of the Si$^{4+}$ ion at large values of $r$ (see Figure 3.14). This replacement can be justified mathematically and shown to reproduce correctly the conduction and valence band states [Cohen89].

Figure 3.14: Schematic plot of a pseudopotential in real space (left) and reciprocal space (right).

The one-electron Schrödinger equation is replaced by a pseudo-wave equation

$$\left ( \frac{p^2}{2m} + V({\ensuremath{\mathitbf{r}}}) \right ) ... ...thitbf{k}}}} \phi_{{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})\ ,$$ (3.101)

with $\phi_{{\ensuremath{\mathitbf{k}}}}({\ensuremath{\mathitbf{r}}})$ denoting the pseudo wave function and $V({\ensuremath{\mathitbf{r}}})$ the pseudopotential. This equation can be used to calculate physical properties of semiconductors which are dependent on the valence and conduction electrons only. Since pseudopotentials are only small perturbations, the energy bands are expected to be similar to those of nearly free electrons and an ansatz where the pseudo wave function is expanded into a sum of plane waves can be used

$$\vert\phi_{{\ensuremath{\mathitbf{k}}}}\rangle = \sum_{{\ensurema... ...{G}}}} \vert{\ensuremath{\mathitbf{k}}} + {\ensuremath{\mathitbf{G}}}\rangle \$$ (3.102)

to diagonalize (3.101). Here, ${\ensuremath{\mathitbf{G}}}$ is a general reciprocal lattice vector as given in (3.24) and Dirac's notation $\vert{\ensuremath{\mathitbf{k}}}+{\ensuremath{\mathitbf{G}}}\rangle$ is applied to denote the plane wave with wave vector ${\ensuremath{\mathitbf{k}}}+{\ensuremath{\mathitbf{G}}}$. The coefficients $a_{{\ensuremath{\mathitbf{G}}}}$ and the eigenvalues $E_{{\ensuremath{\mathitbf{k}}}}$ can be determined from the solution of the secular equation

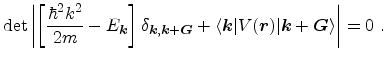$$\det \left \vert \left [\frac{\hbar^2 k^2}{2m} - E_{{\ensuremath{... ...uremath{\mathitbf{k}}} + {\ensuremath{\mathitbf{G}}}\rangle \right \vert = 0\ .$$ (3.103)

The matrix elements of the pseudopotential are given by

$$\langle {\ensuremath{\mathitbf{k}}}\vert V({\ensuremath{\mathitbf... ...G}}} \cdot {\ensuremath{\mathitbf{r}}}}\mathrm{d}{\ensuremath{\mathitbf{r}}}\ .$$ (3.104)

Here, ${\ensuremath{\mathitbf{R}}}$ is a lattice vector in the real lattice, $N$ is the number of atoms in the primitive unit cell^3.2and $\Omega$ denotes its volume. The matrix elements are determined by the Fourier components $V_{{\ensuremath{\mathitbf{G}}}}$ of the pseudopotential

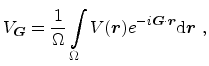$$V_{{\ensuremath{\mathitbf{G}}}} = \frac{1}{\Omega}\int \limits_{\... ...G}}} \cdot {\ensuremath{\mathitbf{r}}}}\mathrm{d}{\ensuremath{\mathitbf{r}}}\ ,$$ (3.105)

which are frequently called form factors of the pseudopotential. If there is more than one atom in the primitive unit cell, a structure factor is introduced which depends on the relative position ${\ensuremath{\mathitbf{r}}}_n$ of the respective atom in the primitive unit cell. The structure factor $S_{{\ensuremath{\mathitbf{G}}}}$ is defined as

$$S_{{\ensuremath{\mathitbf{G}}}}=\frac{1}{N} \sum_n^N e^{-i{\ensuremath{\mathitbf{G}}} \cdot {\ensuremath{\mathitbf{r}}}_n}\ ,$$ (3.106)

where N denotes the number of atoms in the primitive unit cell. The pseudopotential $V({\ensuremath{\mathitbf{r}}})$ can be expressed in terms of the structure factor and the form factors by

$$V({\ensuremath{\mathitbf{r}}}) = \sum_{{\ensuremath{\mathitbf{G}}... ...G}}}} \exp{(i{\ensuremath{\mathitbf{G}}} \cdot {\ensuremath{\mathitbf{r}}})}\ .$$ (3.107)

In crystals with a diamond structure there are two atoms at the positions ${\ensuremath{\mathitbf{r}}}_1$ and ${\ensuremath{\mathitbf{r}}}_2$ in the primitive unit cell. By taking the midpoint between the two atoms in the unit cell as origin, the positions of the atoms are given by ${\ensuremath{\mathitbf{r}}}_1 = \frac{a_0}{8} (1,1,1) = \tau$ and ${\ensuremath{\mathitbf{r}}}_2 = -\frac{a_0}{8} (1,1,1) = -\tau$. Thus, the structure factor is given by

$$S_{{\ensuremath{\mathitbf{G}}}}=\frac{1}{2} \big(\exp(-i{\ensurem... ...ig) = \cos({\ensuremath{\mathitbf{G}}} \cdot {\ensuremath{\mathitbf{\tau}}})\ .$$ (3.108)

In unstrained diamond structures the reciprocal lattice vectors in order of increasing magnitude are (in units of $\frac{2\pi}{a_0}$):

$${\ensuremath{\mathitbf{G}}}_0 = (0,0,0)$$

$${\ensuremath{\mathitbf{G}}}_3 = (1,1,1),\ (\hphantom{-}1,-1,1)\ ,\dots\ ,(-1,-1,-1)$$

$${\ensuremath{\mathitbf{G}}}_4 = (2,0,0),\ ( -2,\hphantom{-}0,0),\ \dots\ ,(\hphantom{-}0,\hphantom{-}0,-2)$$

$${\ensuremath{\mathitbf{G}}}_8 = (2,2,0),\ (\hphantom{-}2,-2,0)\ ,\dots\ ,(\hphantom{-}0,-2,-2)$$

$${\ensuremath{\mathitbf{G}}}_{11} = (3,1,1),\ ( -3,\hphantom{-}1,1)\ ,\dots\ ,(-3,-1,-1)$$

Form factors with reciprocal lattice vectors larger than $G^2 > 11(\frac{2\pi}{a_0})^2$ are neglected, since typically $V_{{\ensuremath{\mathitbf{G}}}}$ decreases as $G^{-2}$ for large ${\ensuremath{\mathitbf{G}}}$ (see Figure 3.14). Assuming that the atomic pseudopotentials are spherically symmetric $V({\ensuremath{\mathitbf{r}}}) = V({\ensuremath{\mathitbf{\vert r\vert}}})$, the form factors only depend on the absolute value of the reciprocal lattice vector. The form factor belonging to ${\ensuremath{\mathitbf{G}}}_0$ shifts the entire energy scale by a constant value, and can therefore be set to zero. The form factors belonging to the reciprocal lattice vectors ${\ensuremath{\mathitbf{G}}}_3$ have an absolute value of $\sqrt 3 \cdot \frac{2\pi}{a_0}$ and are conventionally labeled $V_3$. Since the structure factor of the reciprocal lattice vectors ${\ensuremath{\mathitbf{G}}}_4$ with magnitude $2 \cdot \frac{2\pi}{a_0}$ vanishes,

$$\cos\left ( \frac{2\pi}{a_0} {\ensuremath{\mathitbf{\tau}}} \cdot (\pm 2,0,0)\right ) = \cos\left ( \pm \frac{\pi}{2} \right ) = 0\ ,$$ (3.109)

the respective form factor $V_4$ does not enter the pseudopotential (3.107). Thus, only three pseudopotentials form factors $V_3$, $V_8$ and $V_{11}$ are required to calculate the band structure.

Table 3.5: Parameters employed in the band structure calculation of Si and Ge [Rieger93].

	Silicon	Germanium	Units
$V_{\sqrt{3}}$	-0.2241	-0.221	Rydberg
$V_{\sqrt{8}}$	-0.052	0.019	Rydberg
$V_{\sqrt{11}}$	-0.0724	0.056	Rydberg
$A_l$	0.03	0.275	Rydberg
$R_l$	1.06	1.22	Å
$\mu$	0.00023	0.000965	Rydberg
$\zeta$	7.5589	10.0911	Å$^{-1}$

In Table 3.5 the parameters employed in the empirical pseudopotential calculations are listed. They consist of three local form factors $V_{\sqrt{3}},V_{\sqrt{8}},V_{\sqrt{11}}$, two parameters ($A_0$, $R_0$) to model the nonlocal correction, and two parameters ($\mu$, $\zeta$) entering the spin-orbit interaction term. The parameters coincide with the parameter set provided in [Rieger93] with the exception of $\mu=0.00023$ Ry and $\zeta=7.5589$Å$^{-1}$, which have been adjusted in order to yield the desired split-off energy of 44 meV in the unstrained Si band structure. In the expansion of the pseudo wave function (3.102) plane waves with modulo $\vert{\ensuremath{\mathitbf{G}}}_{lmn} - {\ensuremath{\mathitbf{k}}}\vert < 5.7 (2\pi/a_0)$ were included, which guarantees results converged to approximately 1 meV.

E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology