3.8.2 Inclusion of Strain

To handle general strain conditions, four modifications in the band structure calculation have to be taken into account:

(i) The direct lattice vectors ${{\ensuremath{\mathitbf{a}}}_i}'$ of the strained crystal are calculated by deforming the vectors ${\ensuremath{\mathitbf{a}}}_i$ of the unstrained crystal according to (3.30). From the strained lattice basis vectors, the strained reciprocal lattice vectors ${{\ensuremath{\mathitbf{b}}}_i}'$ can be obtained. These are used to calculate the strained lattice vectors of the reciprocal lattice which are used in the expansion of the pseudo wave function (3.102) and in the calculation of the normalizing volume of the strained unit cell $\Omega_0'$ as given in (3.31).

(ii) Since the local pseudopotential form factors enter the calculation at the strained reciprocal lattice vectors, an interpolation of the pseudopotential is required (see Figure 3.14). Different expressions have been proposed in [Friedel89,Rieger93]. In this work, the pseudopotential form factors of the strained lattice are obtained by performing a cubic spline interpolation through the pseudopotential form factors, $V_0$, $V_3$, $V_8$, $V_{11}$, and $V_{3 k_\mathrm{F}}$. Following [Rieger93], $V_0$ is set to $-2 E_\mathrm{F}/3$, and $V_{3 k_\mathrm{F}}=0$, where $k_\mathrm{F}$ denotes the Fermi wave vector of the free electron gas.

Figure 3.15: Schematic plot of the diamond structure and the primitive unit cell. The central atom at $(\frac {a_0}{4},\frac {a_0}{4},\frac {a_0}{4})$ is indicated by a dark sphere.

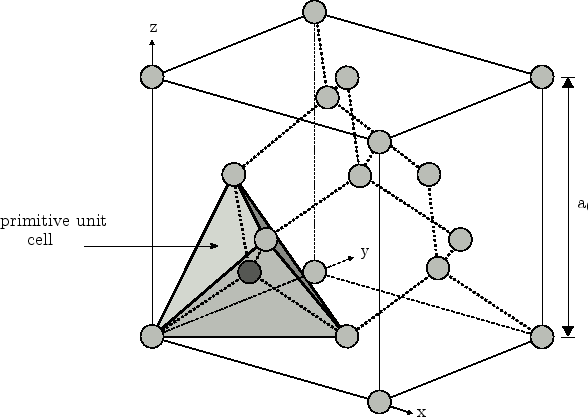
(iii) In Figure 3.15 a schematic plot of the diamond structure with the primitive unit cell is plotted. The latter has a tetragonal shape. The vertex atoms of the tetrahedron and the central atom located at $(\frac {a_0}{4},\frac {a_0}{4},\frac {a_0}{4})$ belong to a different fcc-lattice. While the position of the vertex atoms of the tetrahedron (indicated in light-grey) can be calculated from macroscopic strain, the absolute position of the central atom in the bulk primitive unit cell (dark grey) remains undetermined. To obtain the exact position of the central atom an additional parameter for the displacement has to be taken into account.

Figure 3.16: Unit cell of diamond structure with center atom and its four nearest neighbors. a) In the unstrained crystal, all four bonds are of the same length. b) Under strain, atoms change their positions, leading to different bond lengths. c) The center atom is displaced to adjust a similar distance to the four neighbor atoms, whereas the positions of the vertex atoms is unchanged.

A schematic plot showing the change of atomic positions in the primitive unit cell under strain is given in Figure 3.16. In the unstrained lattice, the central atom is positioned at the center of the tetrahedron, which is indicated by a white circle in Figure 3.16a. Under strain the vertex atoms change their positions and the central atom is displaced from the center of the distorted tetrahedron (see Figure 3.16b). In order to minimize the nearest neighbor central force energy of the system, the central atom moves towards the center of the four vertex atoms. However, opposing this reduction of energy is the increase of nearest neighbor non-central force energy and far-neighbor energy [Kleinman62]. Thus, the central atom does not completely relax to the center of the strained tetrahedron as indicated in Figure 3.16c.

In the case of general strain, the additional displacement of the central atom with respect to the four vertex atoms of the unit tetrahedron in the diamond structure can be modeled in terms of an internal strain parameter (displacement factor) $\xi$: First, the positions of the vertex atoms and the central atom are derived from the macroscopic strain. Then the center of the four vertex atoms is determined. If the internal strain parameter $\xi$ is set to zero, the central atom retains its position determined from the macroscopic strain only; if $\xi=1$ the central atom moves to the center of the four vertex atoms, and all four bonds are of the same length. As previously discussed, neither of the two extrema occurs in a real crystal and a appropriate value $0 \leq \xi \leq 1$ for the internal strain parameter has to be used.

For the determination of the internal strain parameter of Si we performed calculations with the ab-initio total-energy and molecular-dynamics program VASP (Vienna ab-initio simulation program) [Kresse93,Kresse94,Kresse96a,Kresse96b,Kresse99]. A value of $0.5$ was extracted, which is very close to previous theoretical calculations of Nielson [Nielsen85], who extracted a value of 0.53, and the experimental result $0.54 \pm 0.04$ [Cousins87].

If stress is applied along a fourfold axis $\langle 100 \rangle$ no internal displacement occurs. In this case the center of the deformed primitive unit cell coincides with the position of the central atom determined from macroscopic strain and all four bonds are of the same length. For the stress directions $\langle110\rangle$ and $\langle111\rangle$ analytical expressions for the internal displacement can be derived:

• For [110] stress the additional displacement along [001] is given by [Ungersboeck06a]

  $$u_z = -\frac{\xi}{2} \frac{(1+{\ensuremath{\varepsilon_{xx}}}){\ensuremath{\varepsilon_{xy}}}}{1+{\ensuremath{\varepsilon_{zz}}}} a_0\ .$$ (3.110)

  
  

• If the lattice is stressed along $[111]$, the additional displacement is parallel to the stress direction $[111]$

  $${\ensuremath{\mathitbf{u}}} = -\frac{\xi}{2} {\ensuremath{\varepsilon_{xy}}}a_0(1,1,1)\ .$$ (3.111)

  
  

(iv) Finally, strain-induced loss of symmetry gives rise to a change in shape and volume of the irreducible wedge of the first BZ [Ungersboeck06a]. Irreducible wedges under various strain conditions were identified in Section 3.5. Only if the proper wedge is identified, redundancy in the band structure calculations can be avoided.
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology