On (110) oriented substrate, the principal crystallographic system does not
coincide with a system where the  axis is normal to the substrate surface
and a coordinate transformation is necessary to obtain the quantization and
transport masses. From the direction of the substrate normal
axis is normal to the substrate surface
and a coordinate transformation is necessary to obtain the quantization and
transport masses. From the direction of the substrate normal
 |
(4.19) |
the angles
 and
and
 of the coordinate
transformation can be identified. The transformation matrix becomes
of the coordinate
transformation can be identified. The transformation matrix becomes
 |
(4.20) |
The inverse effective mass tensors of the three valley pairs can be
calculated from (4.6)
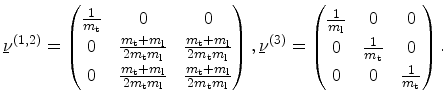 |
(4.21) |
Figure 4.3:
(a) Alignment of constant-energy surfaces of the Si conduction band
with respect to the substrate surface (110). (b) Projection of
constant-energy surfaces onto the (110) plane. Concentric ellipses (unfilled)
indicate the fourfold degeneracy of the unprimed ladder. The constant-energy
lines belonging to the primed ladder are filled in dark grey.
[a] ![\includegraphics[scale=1.0]{inkscape/Cut110_2.eps}](img767.png)
[b] ![\includegraphics[scale=1.5]{inkscape/projectionOr110.eps}](img768.png)
|
It can be seen that the quantization masses
 for the two valley pairs labeled
for the two valley pairs labeled  and
and  in Figure 4.3a are equal. The quantization mass of the remaining
two valleys (labeled
in Figure 4.3a are equal. The quantization mass of the remaining
two valleys (labeled  in Figure 4.3a) is
in Figure 4.3a) is
 . Since
. Since
 , the four valleys with the larger quantization mass
, the four valleys with the larger quantization mass
 belong to the lowest (unprimed) subband ladder, whereas the
two valleys with
belong to the lowest (unprimed) subband ladder, whereas the
two valleys with
 constitute the primed subband ladder. To
calculate the transport masses the eigenvalue problem given in
(4.17) for
constitute the primed subband ladder. To
calculate the transport masses the eigenvalue problem given in
(4.17) for
 has to be solved. On (110) oriented
substrate
has to be solved. On (110) oriented
substrate
 is given by
is given by
 |
(4.22) |
Thus, the transport masses of the unprimed subband ladder
 |
(4.23) |
and the primed ladder
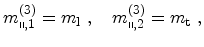 |
(4.24) |
can be obtained. In Figure 4.3b the constant-energy lines of the subbands
for a (110) oriented substrate are shown. The unprimed ladder is fourfold
degenerate, whereas the primed ladder is twofold degenerate. This is opposite
to the situation for (001) oriented substrate, where the unprimed ladder was
twofold degenerate and the primed ladder was fourfold degenerate. The major
principal axis of the unprimed subbands is
![$ [\bar{1}10]$](img777.png) , whereas the major
principal axis of the twofold degenerate primed subband ladder is [001].
, whereas the major
principal axis of the twofold degenerate primed subband ladder is [001].
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
![]() axis is normal to the substrate surface
and a coordinate transformation is necessary to obtain the quantization and
transport masses. From the direction of the substrate normal
axis is normal to the substrate surface
and a coordinate transformation is necessary to obtain the quantization and
transport masses. From the direction of the substrate normal


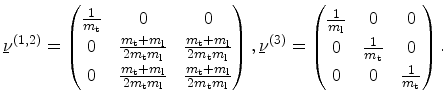
![\includegraphics[scale=1.0]{inkscape/Cut110_2.eps}](img767.png) [b]
[b]![\includegraphics[scale=1.5]{inkscape/projectionOr110.eps}](img768.png)
![]() for the two valley pairs labeled
for the two valley pairs labeled ![]() and
and ![]() in Figure 4.3a are equal. The quantization mass of the remaining
two valleys (labeled
in Figure 4.3a are equal. The quantization mass of the remaining
two valleys (labeled ![]() in Figure 4.3a) is
in Figure 4.3a) is
![]() . Since
. Since
![]() , the four valleys with the larger quantization mass
, the four valleys with the larger quantization mass
![]() belong to the lowest (unprimed) subband ladder, whereas the
two valleys with
belong to the lowest (unprimed) subband ladder, whereas the
two valleys with
![]() constitute the primed subband ladder. To
calculate the transport masses the eigenvalue problem given in
(4.17) for
constitute the primed subband ladder. To
calculate the transport masses the eigenvalue problem given in
(4.17) for
![]() has to be solved. On (110) oriented
substrate
has to be solved. On (110) oriented
substrate
![]() is given by
is given by
