The expression for the scattering probability for electron intravalley
scattering from acoustic phonons can be simplified by using the elastic and
equipartition approximation. Within this approximation, the energy transfer in
a scattering process is neglected, and the phonon population given by the
Bose-Einstein statistics
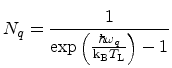 |
(5.16) |
is represented by the equipartition expression
 . Thus, (5.14) becomes
. Thus, (5.14) becomes
![$\displaystyle \{ S_\mathrm{ac}^{\tiny\shortstack{abs \\ [-2pt] emi }} \} ^{v}({...
...ta[E^{v}({\ensuremath{\mathitbf{k}}}') - E^{v}({\ensuremath{\mathitbf{k}}})]\ ,$](img887.png) |
(5.17) |
where  denotes the valley index,
denotes the valley index,
 is the lattice temperature,
is the lattice temperature,
 is the acoustic deformation potential of the
is the acoustic deformation potential of the  -th
valley,
-th
valley,
 is Boltzmann's constant,
is Boltzmann's constant,
 denotes the average
sound velocity, and
denotes the average
sound velocity, and  is the mass density of the crystal.
is the mass density of the crystal.
Since in the elastic approximation no distinction is made between absorption or
emission processes, both transition probabilities can be added. In this
approximation acoustic scattering is isotropic: any state
 belonging
to the equi-energy surface has the same probability of occurrence, independent
of the angle of the initial state
belonging
to the equi-energy surface has the same probability of occurrence, independent
of the angle of the initial state
 . Thus, the rate for acoustic
scattering is a function of energy only
. Thus, the rate for acoustic
scattering is a function of energy only
 |
(5.18) |
where
 is the density of states per spin.
is the density of states per spin.
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology
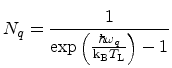
 . Thus, (5.14) becomes
. Thus, (5.14) becomes
![]() belonging
to the equi-energy surface has the same probability of occurrence, independent
of the angle of the initial state
belonging
to the equi-energy surface has the same probability of occurrence, independent
of the angle of the initial state
![]() . Thus, the rate for acoustic
scattering is a function of energy only
. Thus, the rate for acoustic
scattering is a function of energy only
