The deviations of the interface from an ideal flat plane can be described by
a two-dimensional roughness fluctuation,
 , where
, where
 is
the two-dimensional position vector in the plane of the
interface [Ferry97]. The potential associated with the roughness
is
the two-dimensional position vector in the plane of the
interface [Ferry97]. The potential associated with the roughness
 can be viewed as a combination of two effects:
can be viewed as a combination of two effects:
- The boundary perturbation causes the envelope functions to be
displaced from their unperturbed positions.
- The imposed fluctuation of the electric field and the charge density at the
rough interface give rise to an electrostatic contribution to the potential.
The original formulation of Prange and Nee [Prange68] of the unscreened
matrix elements for surface roughness scattering has been adopted. It can be
applied for scattering at two interfaces [Esseni04]
 |
(5.31) |
Here,
 is the momentum transfer,
is the momentum transfer,  is the
quantization mass of electrons in valley
is the
quantization mass of electrons in valley  , and
, and
 denotes the derivative of the envelope function with respect to
denotes the derivative of the envelope function with respect to  at the position of the interface (for instance,
at the position of the interface (for instance,
 , and
, and
 for the front and
back-interface of a thin Si film). The spectral density
for the front and
back-interface of a thin Si film). The spectral density
 is the
2D Fourier transform of the autocovariance function
is the
2D Fourier transform of the autocovariance function
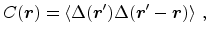 |
(5.32) |
where the brackets denote the ensemble average of the roughness fluctuation
 .
The roughness
spectrum is frequently assumed to be
Gaussian [Jungemann93,Esseni03,Esseni04]
.
The roughness
spectrum is frequently assumed to be
Gaussian [Jungemann93,Esseni03,Esseni04]
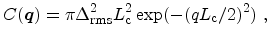 |
(5.33) |
or of exponential shape [Goodnick85,Ferry97]
 |
(5.34) |
Here,
 is the root mean square value of the roughness fluctuations and
is the root mean square value of the roughness fluctuations and
 is the autocovariance length.
is the autocovariance length.
The transition rate for surface roughness scattering is
![$\displaystyle S_{n'n}^{v} ({\ensuremath{\mathitbf{k}}}, {\ensuremath{\mathitbf{...
...'}^{v}({\ensuremath{\mathitbf{k}}}') - E_n^{v}({\ensuremath{\mathitbf{k}}})]\ ,$](img967.png) |
(5.35) |
where intersubband transitions due to surface roughness are restricted to the
same valley [Esseni03,Cheng71]. In the nonparabolic band approximation
the scattering rate for a Gaussian spectrum is given by
Assuming isotropic bands
 ,
the integral over the angle can be written as
,
the integral over the angle can be written as
where
 , and
, and
 denotes the modified Bessel
function of the first kind.
denotes the modified Bessel
function of the first kind.
Since the electrons in the inversion layer screen the scattering potential, the
transition rate for surface roughness scattering is reduced. The dielectric
function relates the unscreened and screened matrix elements of the scattering
potential through the dielectric function

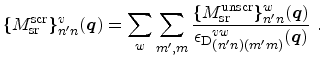 |
(5.38) |
Because surface roughness represents a static potential the dependence on the
frequency  can be dropped. Since the number of relevant subbands can
be of order 100 [Jungemann93], further simplifications are required to
numerically evaluate the impact of screening.
can be dropped. Since the number of relevant subbands can
be of order 100 [Jungemann93], further simplifications are required to
numerically evaluate the impact of screening.
In the long-wavelength limit,
 , intersubband transitions
are completely unscreened [Ferry97], thus
, intersubband transitions
are completely unscreened [Ferry97], thus
 . Furthermore, the multisubband dielectric function reduces to a scalar
function when neglecting the intersubband polarizabilities and the correction
terms due to the intrasubband polarizabilities of the other
subbands [Ferry97]. This approximation is frequently applied for transport
simulations [Esseni03,Esseni04]. The scalar dielectric function for
intrasubband transitions can be given in terms of the polarization function
. Furthermore, the multisubband dielectric function reduces to a scalar
function when neglecting the intersubband polarizabilities and the correction
terms due to the intrasubband polarizabilities of the other
subbands [Ferry97]. This approximation is frequently applied for transport
simulations [Esseni03,Esseni04]. The scalar dielectric function for
intrasubband transitions can be given in terms of the polarization function
 and the form factor
and the form factor

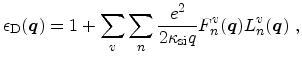 |
(5.39) |
where
 is the dielectric constant of Si [Ferry97]. The
polarization function can be expressed in terms of the Fermi-Dirac distribution
function
is the dielectric constant of Si [Ferry97]. The
polarization function can be expressed in terms of the Fermi-Dirac distribution
function

 |
(5.40) |
The form factor can be calculated from
 |
(5.41) |
Here,  denotes the Green's function. For a semi-infinite Si layer
the Green's function evaluates to [Ando82]
denotes the Green's function. For a semi-infinite Si layer
the Green's function evaluates to [Ando82]
![$\displaystyle G(z,z',q) = \frac{1}{2}\left [\left (1 - \frac{\ensuremath{\kappa...
...{\ensuremath{\kappa_{\mathrm{sio}_2}}}\right ) e^{ q\vert z-z'\vert}\right ]\ .$](img990.png) |
(5.42) |
For a Si layer sandwiched between two semi-infinite SiO films (from
films (from  to
to
 ) it is given by [Fischetti03]
) it is given by [Fischetti03]
![$\displaystyle G(z,z',q) = \frac{1}{(1 - \tilde{\kappa}^2e^{-2qT_\mathrm{si}})} ...
...(e^{q\vert z-z'\vert} + \tilde{\kappa} e^{q\vert z+z'\vert}\right ) \right ]\ ,$](img993.png) |
(5.43) |
where
 .
.
Both the form factors and the polarization function are evaluated numerically
from the wave functions and are used to calculate the screened surface roughness
scattering rate.
Table 5.2:
Parameters for scattering in the 2DEG for {001} and {110}
substrate orientation. For intervalley scattering the bulk parameters of
Table 5.1 are used.
| |
{001} |
{110} |
Units |
 |
14.8 |
13.0 |
eV |
 |
1.3 |
1.5 |
nm |
 |
0.4 |
0.55 |
nm |
E. Ungersboeck: Advanced Modelling Aspects of Modern Strained CMOS Technology

![$\displaystyle S_{n'n}^{v} ({\ensuremath{\mathitbf{k}}}, {\ensuremath{\mathitbf{...
...'}^{v}({\ensuremath{\mathitbf{k}}}') - E_n^{v}({\ensuremath{\mathitbf{k}}})]\ ,$](img967.png)

![$\displaystyle \frac{\ensuremath {\Delta_\mathrm{rms}}^2\ensuremath {L_\mathrm{c...
...n'}^{v}({\ensuremath{\mathitbf{k}}}') - E_n^{v}({\ensuremath{\mathitbf{k}}})] =$](img969.png)




![]()
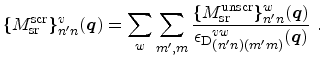
![]() , intersubband transitions
are completely unscreened [Ferry97], thus
, intersubband transitions
are completely unscreened [Ferry97], thus
![]() . Furthermore, the multisubband dielectric function reduces to a scalar
function when neglecting the intersubband polarizabilities and the correction
terms due to the intrasubband polarizabilities of the other
subbands [Ferry97]. This approximation is frequently applied for transport
simulations [Esseni03,Esseni04]. The scalar dielectric function for
intrasubband transitions can be given in terms of the polarization function
. Furthermore, the multisubband dielectric function reduces to a scalar
function when neglecting the intersubband polarizabilities and the correction
terms due to the intrasubband polarizabilities of the other
subbands [Ferry97]. This approximation is frequently applied for transport
simulations [Esseni03,Esseni04]. The scalar dielectric function for
intrasubband transitions can be given in terms of the polarization function
![]() and the form factor
and the form factor
![]()
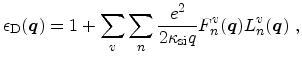
![$\displaystyle G(z,z',q) = \frac{1}{2}\left [\left (1 - \frac{\ensuremath{\kappa...
...{\ensuremath{\kappa_{\mathrm{sio}_2}}}\right ) e^{ q\vert z-z'\vert}\right ]\ .$](img990.png)
![$\displaystyle G(z,z',q) = \frac{1}{(1 - \tilde{\kappa}^2e^{-2qT_\mathrm{si}})} ...
...(e^{q\vert z-z'\vert} + \tilde{\kappa} e^{q\vert z+z'\vert}\right ) \right ]\ ,$](img993.png)