4.1.2 Poisson Equation

The Gauß's law for magnetism (4.4) is satisfied by introduction of the vector potential $\ensuremath{\mathitbf{A}}$ as:

$$\ensuremath{\mathitbf{B}} = \ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\times} \ensuremath{\mathitbf{A}}$$ (4.5)

Inserting (4.5) into (4.2) yields

$$\ensuremath{\mathitbf{E}} = - \frac{\partial \ensuremath{\mathitb... ...}{\partial t} - \ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}} \psi.$$ (4.6)

Substituting this into the relation of the electric displacement and the electric field

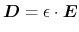$$\ensuremath{\mathitbf{D}} = \ensuremath{\epsilon}\cdot\ensuremath{\mathitbf{E}}$$ (4.7)

results into

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\ensuremat... ...math{\ensuremath{\ensuremath{\mathitbf{\nabla}}}} \psi) = - \ensuremath{\rho}.$$ (4.8)

The permittivity is considered to be homogenous, therefore the first term in (4.8) is zero due to the definition of $\ensuremath{\mathitbf{A}}$ (4.5), so the conventional form of the Poisson equation is obtained:

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\ensuremat... ...math{\ensuremath{\ensuremath{\mathitbf{\nabla}}}} \psi) = - \ensuremath{\rho}.$$ (4.9)

The space charge density $\ensuremath{\rho}$ can be expressed as the product of the elementary charge $\mathrm{q}$ and the sum of the electron $n$ and hole $p$ concentrations and the net concentration of ionized dopants $C_\ensuremath{\mathrm{net}}$:

$$\ensuremath{\rho}= \mathrm{q}\cdot(n - p - C_\ensuremath{\mathrm{net}}).$$ (4.10)

Substituting (4.10) into (4.9) gives:

$$\ensuremath{\ensuremath{\ensuremath{\mathitbf{\nabla}}}\ensuremat... ...hitbf{\nabla}}}} \psi) = \mathrm{q}\cdot(n - p - C_\ensuremath{\mathrm{net}}).$$ (4.11)