



Next: 6.2 Geometric Properties of
Up: 6. Mesh Refinement for
Previous: 6. Mesh Refinement for
The crystal structure of silicon is known as diamond structure which
is adopted by solids with four symmetrically placed covalent bonds. The
diamond structure can be described by a face-centered cubic (FCC) lattice with a
basis of two atoms where one is placed at
 and the other at
and the other at
 ¼
¼ ¼
¼ ¼
¼ ,
where
,
where  is the lattice constant which is about
is the lattice constant which is about
 for relaxed
silicon. Figure 6.1 shows the conventional and the primitive cell of
the diamond structure, where Figure 6.1(a) shows in addition the basis
vectors of the direct lattice, cf. Equation (6.2).
for relaxed
silicon. Figure 6.1 shows the conventional and the primitive cell of
the diamond structure, where Figure 6.1(a) shows in addition the basis
vectors of the direct lattice, cf. Equation (6.2).
Figure 6.1:
Silicon lattice, known as diamond structure is
adopted by solids with four symmetrically placed covalent bonds. The
translational symmetry is a FCC lattice with a basis of two atoms, one at
 an the other at
an the other at
 ¼
¼ ¼
¼ ¼
¼ ,
where
,
where  is the lattice constant.
is the lattice constant.
 |
The lattice structure is invariant under translation in the real space of the
form
 |
(6.1) |
where  ,
, and
and  are integers. The basis vectors of the direct lattice are
are integers. The basis vectors of the direct lattice are
 and and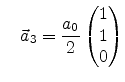 |
(6.2) |
where  denotes the lattice constant, see Figure 6.1(a).
denotes the lattice constant, see Figure 6.1(a).
The set of
reciprocal primitive vectors
 of the lattice
vectors
of the lattice
vectors
 are determined by using matrix
inversion of a column vector representation which reads
are determined by using matrix
inversion of a column vector representation which reads
 |
(6.3) |
The respective general reciprocal lattice vector in
 -space is given by
-space is given by
 |
(6.4) |
where  ,
, and
and  are integers. The basis vectors of the reciprocal lattice
are
are integers. The basis vectors of the reciprocal lattice
are
 |
(6.5) |
with
 . The Wigner-Seitz
cell [113] of the reciprocal lattice, referred as the first Brillouin zone,
is bordered by
. The Wigner-Seitz
cell [113] of the reciprocal lattice, referred as the first Brillouin zone,
is bordered by  faces which can be given as
faces which can be given as
 and and |
(6.6) |
as depicted in Figure 6.2.
Figure 6.2:
The reciprocal lattice structure of a face-centered cubic (FCC) basis
forms a body-centered cubic (BCC) lattice. Figure 6.2(a) shows a
primitive reciprocal lattice part and the Wigner-Seitz cell which is referred as
the first Brillouin zone. Figure 6.2(b) shows the periodicity of the Brillouin zone
cells.
![\begin{figure*}\setcounter{subfigure}{0}
\centering
\subfigure[Reciprocal lattic...
...]
{\epsfig{figure=pics/SI-REC-BZ-ALL.eps,width=0.4\textwidth}}
\end{figure*}](img422.png) |




Next: 6.2 Geometric Properties of
Up: 6. Mesh Refinement for
Previous: 6. Mesh Refinement for
Wilfried Wessner: Mesh Refinement Techniques for TCAD Tools
![]() and the other at
and the other at
![]() ¼
¼![]() ¼
¼![]() ¼
¼![]() ,
where
,
where ![]() is the lattice constant which is about
is the lattice constant which is about
![]() for relaxed
silicon. Figure 6.1 shows the conventional and the primitive cell of
the diamond structure, where Figure 6.1(a) shows in addition the basis
vectors of the direct lattice, cf. Equation (6.2).
for relaxed
silicon. Figure 6.1 shows the conventional and the primitive cell of
the diamond structure, where Figure 6.1(a) shows in addition the basis
vectors of the direct lattice, cf. Equation (6.2).

![]() of the lattice
vectors
of the lattice
vectors
![]() are determined by using matrix
inversion of a column vector representation which reads
are determined by using matrix
inversion of a column vector representation which reads

![]() ,
,![]() and
and ![]() are integers. The basis vectors of the reciprocal lattice
are
are integers. The basis vectors of the reciprocal lattice
are

 and
and
![\begin{figure*}\setcounter{subfigure}{0}
\centering
\subfigure[Reciprocal lattic...
...]
{\epsfig{figure=pics/SI-REC-BZ-ALL.eps,width=0.4\textwidth}}
\end{figure*}](img422.png)