B.1 Euler's Rotation Theorem

According to Euler's rotation theorem [133], any rotation can be described using three rotation angles. If the rotations are written in terms of rotation matrices $\mathbf{A}$ , $\mathbf{B}$ , and $\mathbf{C}$ , then a general rotation $\mathbf{R}$ can be written as

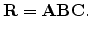$$\mathbf{R} = \mathbf{A}\mathbf{B}\mathbf{C}.$$ (B.1)

The three angles $(\phi ,\theta ,\psi )$ giving the three rotation matrices are called Euler angles. There are several conventions of Euler angles, depending on the axes around which the rotations are carried out. The so-called $x$ -convention, see Figure B.1, is the most common definition. In this convention the rotation is given by Euler angles $(\phi ,\theta ,\psi )$ , where the first rotation is by an angle $\phi$ around the $z$ -axis, the second is by an angle $\theta \in [0,\pi]$ around the $x$ -axis, and the third is by an angle $\psi$ around the $z$ -axis (again).

Figure B.1: Definition of Euler angles $(\phi ,\theta ,\psi )$ in the so-called $x$ -convention rotation scheme according to the rotation components given in Equation (B.2), picture adapted from [133].

In $x$ -convention the component rotations are given by

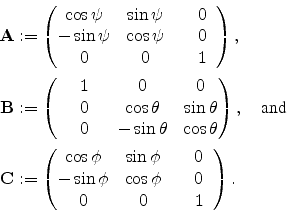$$\begin{split}\mathbf{A}&:= \begin{pmatrix}\cos \psi & \sin \p... ...d 0 \;\;\: \ 0 & 0 & \quad 1 \;\;\: \end{pmatrix}. \end{split}$$ (B.2)

Hence the general $3\times{}3$ rotation matrix $\mathbf{R}$ is given by

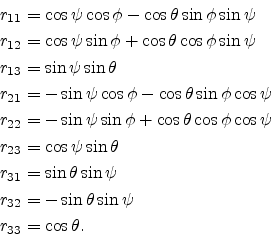$$\begin{split}r_{11} &= \cos \psi \cos \phi - \cos \theta \sin... ...= -\sin \theta \sin \psi \ r_{33} &= \cos \theta . \end{split}$$ (B.3)