



Next: 6.4 BioFET Examples
Up: 6. Generalization of the
Previous: 6.2.6 Buffers and Ionic
6.3 Analytical Comparison between the Poisson-Boltzmann, the Extended Poisson-Boltzmann, and the Debye-Hückel Model
For better comparison between the Poisson-Boltzmann, the extended Poisson-Boltzmann, and the Debye-Hückel model we study their one-dimensional analytical solutions without any charges from macromolecules or due to the site-binding effect at the oxide surface. The surface potential
 will be chosen in a way that all models exhibit the same charge at the surface and that the potential
will be chosen in a way that all models exhibit the same charge at the surface and that the potential  and the electric field
and the electric field
 vanish in the limit of infinite distance away from the surface.
In the first step all equations are transformed to dimensionless units.
vanish in the limit of infinite distance away from the surface.
In the first step all equations are transformed to dimensionless units.
Reformulating the Laplace term
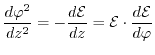 |
(6.14) |
and transforming the equations with
 |
(6.15) |
leads to the following differential equations:
 |
(6.16) |
for the Poisson-Boltzmann model,
 |
(6.17) |
for the extended Poisson-Boltzmann model and
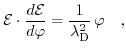 |
(6.18) |
for the Debye-Hückel model.
Assuming vanishing potential  and vanishing electric field
and vanishing electric field
 for large distances
for large distances
 , integrating these equations twice results in the following solutions:
, integrating these equations twice results in the following solutions:
 |
(6.19) |
for the Poisson-Boltzmann model [227],
 |
(6.20) |
or via
 as a function of
as a function of 
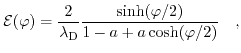 |
(6.21) |
for the extended Poisson-Boltzmann model [225], and
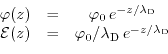 |
(6.22) |
for the Debye-Hückel model [226].
Unfortunately the analytical expression (6.27) is not as handy as the expressions (6.30) for the Debye-Hückel model and (6.25) for the Poisson-Boltzmann model. As can be seen in (6.27), only for the position  as a function of the potential
as a function of the potential  it is possible to write down a compact analytical expression, while for the inverse function one has to use numerical approaches. However, in the limit
it is possible to write down a compact analytical expression, while for the inverse function one has to use numerical approaches. However, in the limit
 the solution for the Poisson-Boltzmann model is recovered [225].
the solution for the Poisson-Boltzmann model is recovered [225].
In the next step we assume an equivalent surface charge
 for all three models, in order to accomplish a better comparison between them. This is realized by choosing an arbitrary charge at the surface and applying Gauß's law. This way, a surface potential
for all three models, in order to accomplish a better comparison between them. This is realized by choosing an arbitrary charge at the surface and applying Gauß's law. This way, a surface potential
 related to the same surface charge can be found.
related to the same surface charge can be found.
The corresponding surface potentials are:
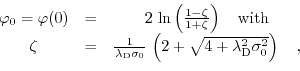 |
(6.23) |
for the Poisson-Boltzmann model [227],
 arccosh arccosh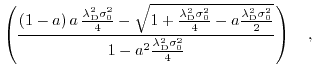 |
(6.24) |
for the extended Poisson-Boltzmann model [225], and
 |
(6.25) |
the Debye-Hückel model, respectively.
Figure 6.5:
Illustrating the different screening characteristica for the Poisson-Boltzmann, the extended Poisson-Boltzmann, and the Debye-Hückel model. In the limit of
 the extended Poisson-Boltzmann model rejoins the Poisson-Boltzmann model, while for increasing closest possible ion distance
the extended Poisson-Boltzmann model rejoins the Poisson-Boltzmann model, while for increasing closest possible ion distance  , which corresponds to a decreasing salt concentration, the screening is reduced and resembles for
, which corresponds to a decreasing salt concentration, the screening is reduced and resembles for  the Debye-Hückel model.
the Debye-Hückel model.
|
|
Fig. 6.5 shows a comparison between the Poisson-Boltzmann, the extended Poisson-Boltzmann, and the Debye-Hückel model. As already mentioned before, one can see that for
 the extended Poisson-Boltzmann model and the Poisson-Boltzmann model coincide. Increasing the closest possible approach
the extended Poisson-Boltzmann model and the Poisson-Boltzmann model coincide. Increasing the closest possible approach  between two ions, leads to a reduction in screening and thus higher surface potential
between two ions, leads to a reduction in screening and thus higher surface potential
 . Furthermore, for
. Furthermore, for  the extended Poisson-Boltzmann model equations quite well with the Debye-Hückel model. This shows that the extended Poisson-Boltzmann model is able to cover a wider range of screening behavior than the Poisson-Boltzmann and the Debye-Hückel model.
the extended Poisson-Boltzmann model equations quite well with the Debye-Hückel model. This shows that the extended Poisson-Boltzmann model is able to cover a wider range of screening behavior than the Poisson-Boltzmann and the Debye-Hückel model.




Next: 6.4 BioFET Examples
Up: 6. Generalization of the
Previous: 6.2.6 Buffers and Ionic
T. Windbacher: Engineering Gate Stacks for Field-Effect Transistors
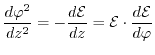
![]() and vanishing electric field
and vanishing electric field
![]() for large distances
for large distances
![]() , integrating these equations twice results in the following solutions:
, integrating these equations twice results in the following solutions:
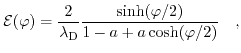
![]() as a function of the potential
as a function of the potential ![]() it is possible to write down a compact analytical expression, while for the inverse function one has to use numerical approaches. However, in the limit
it is possible to write down a compact analytical expression, while for the inverse function one has to use numerical approaches. However, in the limit
![]() the solution for the Poisson-Boltzmann model is recovered [225].
the solution for the Poisson-Boltzmann model is recovered [225].
![]() for all three models, in order to accomplish a better comparison between them. This is realized by choosing an arbitrary charge at the surface and applying Gauß's law. This way, a surface potential
for all three models, in order to accomplish a better comparison between them. This is realized by choosing an arbitrary charge at the surface and applying Gauß's law. This way, a surface potential
![]() related to the same surface charge can be found.
related to the same surface charge can be found.
![\includegraphics[width=0.8\textwidth]{figures/screening_new3.ps}](img916.png)
![]() the extended Poisson-Boltzmann model and the Poisson-Boltzmann model coincide. Increasing the closest possible approach
the extended Poisson-Boltzmann model and the Poisson-Boltzmann model coincide. Increasing the closest possible approach ![]() between two ions, leads to a reduction in screening and thus higher surface potential
between two ions, leads to a reduction in screening and thus higher surface potential
![]() . Furthermore, for
. Furthermore, for ![]() the extended Poisson-Boltzmann model equations quite well with the Debye-Hückel model. This shows that the extended Poisson-Boltzmann model is able to cover a wider range of screening behavior than the Poisson-Boltzmann and the Debye-Hückel model.
the extended Poisson-Boltzmann model equations quite well with the Debye-Hückel model. This shows that the extended Poisson-Boltzmann model is able to cover a wider range of screening behavior than the Poisson-Boltzmann and the Debye-Hückel model.