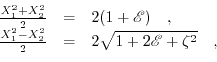A. Re-expressing X₁ as a Function of X₂

In the first step the Hamiltonian (4.1) and the energy dispersion (4.4) are transformed into dimensionless units with the expressions:

$$\begin{array}{cc} X = \frac{k_{z}}{k_{0}}\, , & E_{0}=\frac{\... ...rac{E}{E_{0}}\, ,& \zeta = \frac{\delta}{E_{0}}\, . \end{array}$$ (7.1)

The energy dispersion then takes the following form:

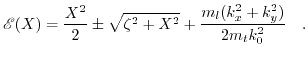$$\mathscr{E}(X) = \frac{X^{2}}{2} \pm \sqrt{\zeta^{2} + X^{2}}+ \frac{m_{l} ( k_{x}^{2} + k_{y}^{2} )}{2 m_{t} k_{0}^{2}}\quad.$$ (7.2)

Setting the determinant of the dimensionless Hamiltonian to zero allows to express $X$ as a function of energy $\mathscr{E}$:

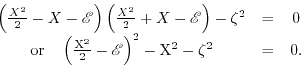$$\begin{array}{ccc} \left( \frac{X^{2}}{2} - X - \mathscr{E}\r... ...mathscr{E}\right)^{2} - X^{2} - \zeta^{2}&=&0 \quad.\end{array}$$ (7.3)

Re-expressing the fourth order equation (7.3) as a second order equation $\frac{\nu^{2}}{4}-\nu\mathscr{E}+\mathscr{E}^{2}-\nu-\zeta^{2}=0$ by

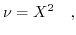$$\nu=X^{2}\quad,$$ (7.4)

we find the solution,

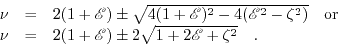$$\begin{array}{ccc} \nu& =& 2(1+\mathscr{E}) \pm \sqrt{4(1+\ma... ...cr{E}) \pm 2\sqrt{1+2\mathscr{E}+ \zeta^{2}} \quad. \end{array}$$ (7.5)

This formulation preserves all four solutions for $X$. Embracing two sets of $X$ values in two separate equations leads to the following expressions:

$$\begin{array}{ccc} \nu& =& \left(1\pm\sqrt{1+2\mathscr{E}+\ze... ...+2\mathscr{E}+\zeta^{2}}\right)^{2}-\zeta^{2}\quad. \end{array}$$ (7.6)

Using the following identities:

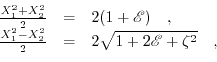$$\begin{array}{ccc} \frac{X_{1}^{2}+X_{2}^{2}}{2} &=& 2 (1+\ma... ...}}{2} &=& 2 \sqrt{1 + 2 \mathscr{E}+ \zeta^2}\quad, \end{array}$$ (7.7)

leads to the desired expressions $X_{1}(X_{2})$ and $X_{2}(X_{1})$.

$$\begin{array}{ccc} X_{1}^{2} &=& \left(1+\frac{X_{1}^{2}-X_{2... ...& X_{1}^{2} +4 - 4 \sqrt{X_{1}^{2}+\zeta^{2}}\quad. \end{array}$$ (7.8)

The transformation to dimensionless units of the corresponding expression for $c(X)$ is:

$$c(X) = - \frac{X}{\zeta \pm \sqrt{\zeta^2 + X^{2}}}\quad.$$ (7.9)